Study of Stability and Vibration Reduction in Multi-Tool Ultrasonic Machining under Simultaneous Primary and Internal Resonance ()
1. Introduction
Ultrasonic machining (USM) is of particular interest for the machining of non-conductive, brittle materials such as engineering ceramics. Rupinder and Aspinwall [1,2] introduced a review for the fundamental principles of stationary ultrasonic machining, the material removal mechanisms involved and the effect of operating parameters on material removal rate, tool wear rate, and work piece surface finish of titanium and its alloys for application in manufacturing industry. The USM mechanism is dependent on vibration control of the machine head at resonance, while the tool represented by a dynamic absorber is doing the machining. Lim et al. [3] studied the behavior of the (USM) hypothesized theoretical model. The theoretical results showed that controlled variations in the softening stiffness can have a significant effect on the overall non-linear response of the system, by making the overall effect hardening, softening, or approximately linear. Experimentally, it has also been demonstrated that coupling of ultrasonic components with different non-linear characteristics can strongly influence the performance of the system. Amer [4] investigated the coupling of two non-linear oscillators of the main system and absorber representing ultrasonic cutting process subjected to parametric excitation forces. A threshold value of main system linear damping has been obtained, where vibration can be reduced dramatically. This threshold value can be used effectively for passive vibration control, if it is economical. This will be more useful than usual passive control, and active control. It can be applicable for all excitation frequencies. Asfar, Eissa, El-Bassiouny and Shitikova [5-16] showed how effective is the passive vibration control reduction at resonance. Eissa, El-Bassiouny and Jaensch [17-23] showed how effective is the active control in vibration reduction at resonance at different modes of vibration. They demonstrated the advantages of active control over the passive one. Eissa et al. [24-26] investigated saturation phenomena in non-linear oscillating systems subject to multi-parametric and/or external excitations. The system represents the vibration of a single-degree-of-freedom cantilever or the wing of an aircraft. They reported the occurrence of saturation phenomena at different parameters values. They applied saturation values of different parameters as optimum working conditions for vibration suppression of the cantilever. El Ganaini et al. [27-29] studied USM model subject to multi-external or both multi-external and multi-parametric and both multiexternal and tuned excitation forces. The model consists of multi-degree-of-freedom system consisting of the tool holder and absorbers (tools) simulating ultrasonic machining process. The advantages of using multi-tools are to machine different materials and different shapes at the same time. This leads to time saving and higher machining efficiency. Besides, devoting all the available energy in the cutting process. The multiple time scale perturbation technique is applied throughout to get an approximate solution up to the second order approximation. The stability of the system is investigated applying both phaseplane and frequency response function methods. The effects of the different parameters of the absorbers on system behavior are studied numerically. The objective of this work is to study the model subject to multi-external excitation forces. The model is represented by a fourdegree-of-freedom system consisting of the main system (machine head) and three absorbers (tools) simulateing ultrasonic machining process. The multiple time scale perturbation technique is applied throughout to get an approximate solution up to the second order approximation. The stability of the system is investigated applying both phase-plane and frequency response functions. The effects of the different parameters of the absorber on system behavior are studied numerically. Comparison with the available published work is reported.
2. Mathematical Modeling
The considered model is shown schematically in Figure 1, while Figure 2 illustrates the principles of USM. It consists of the tool holder and absorbers (tools) simulating multi-tool ultrasonic machining process represented by a multi-degree-of-freedom non-linear system. The main system is exited by multi-external forces as shown in the following equations:
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)


Figure 2. Response of the main system and absorbers at simultaneous primary and internal resonance case  .
.
2.1. Perturbation Analysis
Multiple scale perturbation method is conducted to obtain an approximate solution for equations (1)-(4). Assuming the solution in the form:
 (5)
(5)
and the time derivatives became
 (6)
(6)
where Tn = ent. (n = 0, l) are the fast and slow time scales respectively.
Substituting Equations (5) and (6) into Equations (1)- (4), and equating the coefficients of the same power of ein both sides, we obtain
 (7)
(7)
 (8)
(8)

(9)
 (10)
(10)
 (11)
(11)
 (12)
(12)
The solution of Equation (7) can be expressed in the form
 (13)
(13)
Using Equation (13) into Equation (8) yields
 (14)
(14)
where ,
,  are complex functions in
are complex functions in
 , which can be determined from eliminating the secular terms at the next approximation, and cc, stands for the conjugate of the preceding terms. Substituting Equations (13) and (14) into Equation (9), eliminating the secular terms, then the first order approximation is given by:
, which can be determined from eliminating the secular terms at the next approximation, and cc, stands for the conjugate of the preceding terms. Substituting Equations (13) and (14) into Equation (9), eliminating the secular terms, then the first order approximation is given by:

(15)
where  and
and  are complex functions in
are complex functions in . From Equations (13)-(15) into equations (10)-(12) and eliminating the secular terms to obtain the solutions are given by:
. From Equations (13)-(15) into equations (10)-(12) and eliminating the secular terms to obtain the solutions are given by:

(16)

(17)

(18)
where ,
,  ,
,  and
and  are complex functions in
are complex functions in .
.
The reported resonance cases at this approximation order are:
1) Trivial resonance: . Primary resonance:
. Primary resonance:

2) Sub-harmonic resonance:

3) Super-harmonic resonance:



4) Internal resonance: ,
,
 ,
,

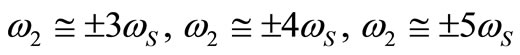 ,
,

 ,
,

 ,
,



5) Combined resonance:
 ,
,

6) Simultaneous or incident resonance: Any combination of the above resonance cases is considered as simultaneous resonance.
2.2. Numerical Results
Table 1 illustrates the selected values of the equations parameters used in resonance case calculations and its units.
Table 2 summarizes some of different resonance cases and the effectiveness of the absorbers.
Figure 2 illustrates the response for the system with absorber at the simultaneous primary resonance  . The effectiveness of the absorber Ea (the steady state amplitude of the main system without absorber/the steady state amplitude of main system with absorber) is about 7, which means that the maximum amplitude is reduced to about 14% of its original value.
. The effectiveness of the absorber Ea (the steady state amplitude of the main system without absorber/the steady state amplitude of main system with absorber) is about 7, which means that the maximum amplitude is reduced to about 14% of its original value.
3. Results and Discussion
One of the effective resonance cases where the tool holder has low amplitude and at the same time, the absorbers have high amplitudes is studied in the next section.
3.1. Stability of the System
Introducing the detuning parameters ,
,  ,
,  and
and  in the primary and internal resonance to convert the small-divisor terms into the secular terms, according to:
in the primary and internal resonance to convert the small-divisor terms into the secular terms, according to:
 (19)
(19)

Table 1. The values of the equations parameters.

Table 2. summarizes the resonance cases for the tool holder and absorber.
This case represent the system best case and at the same time absorber high amplitude. Substituting equation (19) into equations (9)-(12) and eliminating the secular terms, leads to the solvability conditions for the first order approximation noting that ,
,  ,
,  and
and  are functions in
are functions in 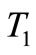 we get
we get

(20)
 (21)
(21)
 (22)
(22)
 (23)
(23)
Putting  ,
, (24)
(24)
where  and
and  are the steady state amplitudes and the phases of the motion respectively. Substituting Equation (24) into Equations (20)-(23) and separating real and imaginary part yields,
are the steady state amplitudes and the phases of the motion respectively. Substituting Equation (24) into Equations (20)-(23) and separating real and imaginary part yields,
 (25)
(25)
 (26)
(26)
 (27)
(27)
 (28)
(28)
 (29)
(29)
 (30)
(30)
 (31)
(31)
 (32)
(32)
where:  are defined in the appendix,
are defined in the appendix,
 (33)
(33)
For steady state solutions,  ,
, .
.
Then from Equation (33), we get:
 (34)
(34)
Then it follows from equations (25)-(32) that the steady state solutions are given by:
 (35)
(35)
 (36)
(36)
 (37)
(37)
 (38)
(38)
 (39)
(39)
 (40)
(40)
 (41)
(41)
 (42)
(42)
From Equations (35)-(42) we have the following case:
(practical case) 
Table 3 gives the final results of the frequency response equations (in Table 3), where 
 and
and  are real functions. The stability of the linear solution of the obtained fixed points will be determined as follows. Consider
are real functions. The stability of the linear solution of the obtained fixed points will be determined as follows. Consider  in the form:
in the form:
 (43)
(43)

Table 3. Frequency response equations.
where 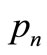 and
and  are real and
are real and ,
,  ,
,  and
and . Substituting equation (43) into the linear part of equations (20)-(23) and separating real and imaginary part yields,
. Substituting equation (43) into the linear part of equations (20)-(23) and separating real and imaginary part yields,
 (44)
(44)
 (45)
(45)
 (46)
(46)
 (47)
(47)
 (48)
(48)
 (49)
(49)
 (50)
(50)
 (51)
(51)
The eigenvalues of the above system of equations are given by the equation
 (52)
(52)
where,  are functions in the parameters (
are functions in the parameters (
 ,
, ,
,


 ). According to the Routh-Huriwitz criterion, the necessary and sufficient conditions for all the roots of equation (52) to possess negative real parts if, and only if,
). According to the Routh-Huriwitz criterion, the necessary and sufficient conditions for all the roots of equation (52) to possess negative real parts if, and only if,
 (53)
(53)
and all its principle minors are positive.  are real functions.
are real functions.
3.2. Numerical Results
Figures 3(a) and 4(a) shows that the effects of the detuning parameters  and
and  on the steady state amplitudes of the main system
on the steady state amplitudes of the main system  and absorbers
and absorbers ,
,  and
and  for the stability of the practical case where
for the stability of the practical case where  and
and . For different values of the damping coefficients
. For different values of the damping coefficients , the non-linear parameters
, the non-linear parameters , (n = 1, 2, 3,4 ) and the non-linear parameters
, (n = 1, 2, 3,4 ) and the non-linear parameters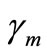 , (m = 2, 3, 4) the effects are trivial as shown in Figure 3(b). From Figure 3(c) we find that the steady state amplitude of the tool holder is a monotonic increasing function in its excitation amplitude
, (m = 2, 3, 4) the effects are trivial as shown in Figure 3(b). From Figure 3(c) we find that the steady state amplitude of the tool holder is a monotonic increasing function in its excitation amplitude  with an increase
with an increase
in the unstable region of the solution.
The steady state amplitude of the tool holder is a monotonic decreasing function in the natural frequencies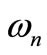 , (n = 1, 2, 3, 4) with a decrease in the unstable region of the solution as shown in Figure 3(d).
, (n = 1, 2, 3, 4) with a decrease in the unstable region of the solution as shown in Figure 3(d).
Now the effect of the detuning parameters  and
and  on the steady state amplitude of the tools
on the steady state amplitude of the tools  and
and  is shown in Figure 4(a).
is shown in Figure 4(a).
For different values of the damping coefficients , (i = 6, 7, 8), the effects on the steady state amplitudes of the tools are trivial as shown in Figure 4(b). For different values of the non-linear parameters
, (i = 6, 7, 8), the effects on the steady state amplitudes of the tools are trivial as shown in Figure 4(b). For different values of the non-linear parameters , (s = 5, 6, 7), the steady state amplitude of the tools are monotonic increasing as shown in Figure 4(c). Figure 4(d) shows that the steady state amplitude of the tools is a monotonic decreasing function in the natural frequencies
, (s = 5, 6, 7), the steady state amplitude of the tools are monotonic increasing as shown in Figure 4(c). Figure 4(d) shows that the steady state amplitude of the tools is a monotonic decreasing function in the natural frequencies , (m = 2, 3, 4) and the region of unstable solution is decreasing. For all figures no jump phenomena was observed.
, (m = 2, 3, 4) and the region of unstable solution is decreasing. For all figures no jump phenomena was observed.
4. Conclusions
The vibrations of a four-degree-of-freedom non-linear mechanical system and absorbers are investigated. The physical motivation for the system stems from applications in ultrasonic machining in which an exciter (machine head) drives tuned blades (absorbers) having both linear and cubic non-linearities. In the present work, we considered multi-tools which allow the machining of different materials and different shapes in different or one workpiece the vibration of ultrasonic machine head can be controlled via non-linear absorbers. Multiple time scale perturbation technique is applied to determine semi-closed form solutions for the coupled deferential equations describing the system up to the second order approximations. To study the stability of the system, both the frequency response equations and the phase-plane technique are applied. From the above study the following may be concluded.
1) Optimum working conditions at 
 , where the vibration of the tool holder is suppressed to about 12.5% of the original amplitude, and the three tools have reasonable amplitudes.
, where the vibration of the tool holder is suppressed to about 12.5% of the original amplitude, and the three tools have reasonable amplitudes.
2) For different values of the damping coefficients , the non-linear parameters
, the non-linear parameters , (n = 1,2,3,4) and the non-linear parameters
, (n = 1,2,3,4) and the non-linear parameters , (m = 2, 3, 4) we find the effects of these parameters on the steady state amplitude of the tool holder are trivial and same effects have been
, (m = 2, 3, 4) we find the effects of these parameters on the steady state amplitude of the tool holder are trivial and same effects have been
obtained for the damping coefficients , (i = 6, 7, 8) on the steady state amplitude of the three tools.
, (i = 6, 7, 8) on the steady state amplitude of the three tools.
3) The steady state amplitude of the tool holder is a monotonic decreasing function in the natural frequencies , (n =1, 2, 3, 4) with decreasing in the region of unstable solution.
, (n =1, 2, 3, 4) with decreasing in the region of unstable solution.
4) The steady state amplitude of the tool holder is a monotonic increasing function in its excitation amplitude  with increasing in the region of unstable solution.
with increasing in the region of unstable solution.
5) The steady state amplitude of the tools is a monotonic decreasing function in the non-linear parameters , (s = 5, 6, 7) and the natural frequencies
, (s = 5, 6, 7) and the natural frequencies , (m = 2, 3, 4) and the region of unstable solution is decreasing.
, (m = 2, 3, 4) and the region of unstable solution is decreasing.
6) To make use of machine capability, multi-tools are used to save both time and power.
7) The reported results are in a good agreement with References [3,4] regarding the amplitude reduction.
Nomenclature
 , (n = 1, 2, 3, 4). The damping coefficients of the system and the absorber.
, (n = 1, 2, 3, 4). The damping coefficients of the system and the absorber.
 , (m = 1, 2, 3, 4). The stiffness of the system and the absorbers.
, (m = 1, 2, 3, 4). The stiffness of the system and the absorbers.
 , (m = 1, 2, 3, 4). The non-linear parameters of the system and the absorber.
, (m = 1, 2, 3, 4). The non-linear parameters of the system and the absorber.
 ,
, 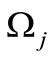 (j = 1, 2, 3). The excitation amplitudes and frequencies.
(j = 1, 2, 3). The excitation amplitudes and frequencies.
 . The masses of the system and the absorber.
. The masses of the system and the absorber.
 , (n = 1, 2, 3, 4). The linear damping factors of the system.
, (n = 1, 2, 3, 4). The linear damping factors of the system.
 The quadratic damping factors of the system.
The quadratic damping factors of the system.
 The damping factors of the absorbers.
The damping factors of the absorbers.
 , (m = 1, 2, 3, 4). The coupling non-linear parameters of the system.
, (m = 1, 2, 3, 4). The coupling non-linear parameters of the system.
 The non-linear parameters of the absorbers.
The non-linear parameters of the absorbers.
 , (s = 1, 2, 3, 4). The natural frequencies of the system and absorbers.
, (s = 1, 2, 3, 4). The natural frequencies of the system and absorbers.
 The stiffness of the system.
The stiffness of the system.
 , i = (1, 2, 3, 4). Displacement of both system and absorber.
, i = (1, 2, 3, 4). Displacement of both system and absorber.
Appendix
