A Fixed-Phase Quantum Search Algorithm with More Flexible Behavior ()
1. Introduction
Grover’s quantum search algorithm [1] is one of the most important developments in quantum computation. For searching a marked state in an unordered database, it achieves quadratic speed up over classical search algorithms. At present, Grover’s quantum search algorithm has been greatly noticed and has become a challenging research field. However, the Grover’s algorithm also has some limitations. When the fraction of marked items is greater than a quarter of the total items in the database, the success probability will rapidly decrease, and when the fraction of marked items is greater than half of the total items in the database, the algorithm will be disabled.
Up to now, many efforts in improving Grover’s originnal algorithm have been done. The Grover’s original algorithm consists of inversion of the amplitude in the desired state and inversion-about-average operation [1]. In [2], Grover presented a general algorithm:
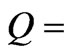 , where U is any unitary operation,
, where U is any unitary operation,  is the adjoint of U,
is the adjoint of U,  ,
,  ,
,  is an initial state and
is an initial state and 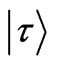 is a desired state. When
is a desired state. When , where W is the Walsh-Hadamard transformation, and
, where W is the Walsh-Hadamard transformation, and , the general algorithm becomes the original algorithm. Long extended Grover’s algorithm [3]. In Long’s algorithm,
, the general algorithm becomes the original algorithm. Long extended Grover’s algorithm [3]. In Long’s algorithm,  and
and  are expressed as
are expressed as  and
and , respectively. Long further studied two-phase matching conditions [4]. When
, respectively. Long further studied two-phase matching conditions [4]. When , Long’s algorithm becomes Grover’s original algorithm. In [5], Grover presented the new algorithm by replacing the selective inversions by selective phase shifts of
, Long’s algorithm becomes Grover’s original algorithm. In [5], Grover presented the new algorithm by replacing the selective inversions by selective phase shifts of . Just like classical search algorithms the algorithm has a fixed point in state-space toward which it preferentially converges. Li et al. studied the changes of the approximation error in the fixed-point search algorithm obtained by replacing equal phase shifts of
. Just like classical search algorithms the algorithm has a fixed point in state-space toward which it preferentially converges. Li et al. studied the changes of the approximation error in the fixed-point search algorithm obtained by replacing equal phase shifts of  by different phase shifts [6]. In [7], by applying Partial Diffusion Operator, Younes et al. proposed a quantum search algorithm and showed that the performance of the algorithm is more reliable than other quantum search algorithms especially for multiple matches within the search space. The minimum success probability of this algorithm is 84.72% when
by different phase shifts [6]. In [7], by applying Partial Diffusion Operator, Younes et al. proposed a quantum search algorithm and showed that the performance of the algorithm is more reliable than other quantum search algorithms especially for multiple matches within the search space. The minimum success probability of this algorithm is 84.72% when  . In [8], by regarding the searching engine as a three-dimensional rotation in the SO(3) picture, Long presented a modified version of Grover’s algorithm that searches a marked state with full successful probability. However, two phase shifts in Long’s algorithm are determined by the number of iterations and the number of marked items, not a fixed value. Building quantum devices using fixed operators is a must to simplify the hardware construction. Quantum search engine is not an exception [9]. Therefore, this algorithm is not conducive to the quantum computer hardware implementation. Yonues presented a fixed phase quantum search algorithm in [9]. By selecting phase shifts of
. In [8], by regarding the searching engine as a three-dimensional rotation in the SO(3) picture, Long presented a modified version of Grover’s algorithm that searches a marked state with full successful probability. However, two phase shifts in Long’s algorithm are determined by the number of iterations and the number of marked items, not a fixed value. Building quantum devices using fixed operators is a must to simplify the hardware construction. Quantum search engine is not an exception [9]. Therefore, this algorithm is not conducive to the quantum computer hardware implementation. Yonues presented a fixed phase quantum search algorithm in [9]. By selecting phase shifts of  in the standard amplitude amplification, the success probability of at least 98% is obtained in
in the standard amplitude amplification, the success probability of at least 98% is obtained in , which is better than other fixed operator quantum search algorithms. In [10], a novel information geometric characterization of Grover’s quantum search algorithm is presented, and the possible deviations from Grover’s algorithm within this quantum information geometric setting are discussed. In [11], a method for implementing the Grover search algorithm based on multi-level systems is proposed.
, which is better than other fixed operator quantum search algorithms. In [10], a novel information geometric characterization of Grover’s quantum search algorithm is presented, and the possible deviations from Grover’s algorithm within this quantum information geometric setting are discussed. In [11], a method for implementing the Grover search algorithm based on multi-level systems is proposed.
The methods mentioned above cannot solve the problem that the algorithm efficiencies decrease as the marked items increase. In this paper, we study the phase matching in Grover’s algorithm, and propose an adaptive matching, namely,  , where λ is the fraction of marked items, and
, where λ is the fraction of marked items, and  is the polynomial for λ. With application of the new phase matching, when λ is a rational number in range
is the polynomial for λ. With application of the new phase matching, when λ is a rational number in range  to 1/4, the probability of getting correct results is equal to 1 with two Grover iterations, and when λ is greater than 1/4, the probability of getting correct results is equal to 1 with only one Grover iteration.
to 1/4, the probability of getting correct results is equal to 1 with two Grover iterations, and when λ is greater than 1/4, the probability of getting correct results is equal to 1 with only one Grover iteration.
In this letter, with application of two operators with arbitrary phase rotations in [3] and the phase matching conditions in [4], we will present a general Grover algorithm with fixed-phased shifts. The different algorithms can be derived from this algorithm according to the different phase shifts. When the phase shifts are fixed at , the success probability of at least 99.38% can be obtained in
, the success probability of at least 99.38% can be obtained in  iterations.
iterations.
2. Grover’s Algorithm and Its Problem
2.1. Grover’s Algorithm Summary
Suppose we wish to search through a search space of N elements. Rather than search the elements directly, we concentrate on the index to those elements, which is just a number in range 0 to N – 1. For convenience we assume N = 2n, so the index can be stored in n qubits, and that the search problem has exactly M solutions, with . The algorithm begins with the state
. The algorithm begins with the state . The Walsh-hadamard transform is used to put the state
. The Walsh-hadamard transform is used to put the state  in the equal superposition state,
in the equal superposition state,
 . (1)
. (1)
The Grover quantum search algorithm then consists of repeated application of a quantum subroutine, know as the Grover iteration or Grover operator, which we denote G. The Grover iteration may be broken up into four steps.
1) Apply the oracle O. The oracle is a unitary operator defined by its action on the computational basis
 , (2)
, (2)
where  is the index register,
is the index register,  denotes addition modulo 2, and the oracle qubit
denotes addition modulo 2, and the oracle qubit  is a single qubit which is flipped if
is a single qubit which is flipped if , and is unchanged otherwise.
, and is unchanged otherwise.
2) Applying the Walsh-Hadamard transform .
.
3) Perform a conditional phase shift, with every computational basis state except  receiving a phase shift of –1,
receiving a phase shift of –1, .
.
4) Applying the Walsh-Hadamard transform .
.
It is useful to note that the combined effect of steps 2), 3), and 4) is
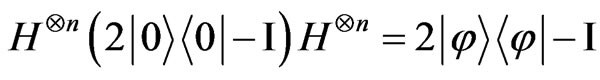 , (3)
, (3)
where  is the equally weighted superposition of states, (1). Thus the Grover iteration, G, may be written as
is the equally weighted superposition of states, (1). Thus the Grover iteration, G, may be written as .
.
Let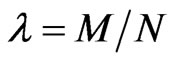 , and CI(x) denote the integer closest to the real number x, where by convention we round halves down. Then repeating the Grover iteration
, and CI(x) denote the integer closest to the real number x, where by convention we round halves down. Then repeating the Grover iteration
 (4)
(4)
times rotates  to within an angle
to within an angle  of a superposition of marked states [12]. Observation of the state in the computational basis then yields a solution to the search problem with probability at least one-half.
of a superposition of marked states [12]. Observation of the state in the computational basis then yields a solution to the search problem with probability at least one-half.
2.2. Grover’s Algorithm Success Probability
In fact, the Grover iteration can be regarded as a rotation in the two-dimensional space spanned by the starting vector  and the state consisting of a uniform superposition of solutions to the search problem. Let
and the state consisting of a uniform superposition of solutions to the search problem. Let  represent a normalized states of a sum over all which are not solutions to the search problem, and
represent a normalized states of a sum over all which are not solutions to the search problem, and  represent a normalized states of a sum over all which are solutions to the search problem. Simple algebra shows that the initial state
represent a normalized states of a sum over all which are solutions to the search problem. Simple algebra shows that the initial state  may be re-expresses as
may be re-expresses as
 , (5)
, (5)
where . After R Grover iterations, the initial state is taken to
. After R Grover iterations, the initial state is taken to
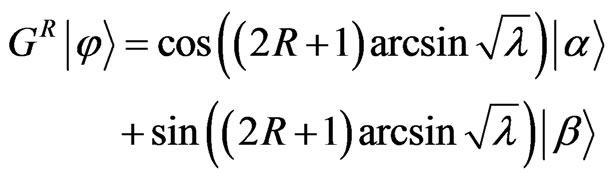 . (6)
. (6)
Hence, the success probability is
 . (7)
. (7)
The curve of P is shown in Figure 1.
2.3. The Drawback of Grover’s Algorithm
It is easy to deduce from Equations (4) and (7) that when
 ,
,  decreases rapidly. When
decreases rapidly. When ,
,  increases rapidly. When
increases rapidly. When

Figure 1. The success probability of Grover’s algorithm.
 ,
,  decreases rapidly. When
decreases rapidly. When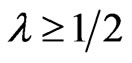 , there is
, there is ,
,  , and the algorithm is disabled. Hence, the Grover’s algorithm is no longer useful when
, and the algorithm is disabled. Hence, the Grover’s algorithm is no longer useful when .
.
The reason for the problem is that the two phase rotations in Grover iteration are fully equivalent in both amplitude and direction, namely π. According to [12], the result of such phase rotations is that, for the one Grover iteration, the phase of the  increases
increases  radians, and that rotating through at least
radians, and that rotating through at least  radians takes the
radians takes the  to
to . When
. When , there are only
, there are only  and
and  make R an integer, namely,
make R an integer, namely,
 ,
, .
.
3. The Grover Algorithm with Fixed-Phase Shifts
3.1. The Searching Engine Description
Assume that  denote the marked states, and that
denote the marked states, and that  denote the nonmarked states. Let
denote the nonmarked states. Let

and , then the initial system can be written as follows,
, then the initial system can be written as follows,
 . (8)
. (8)
Two phase shifting operator in Grover’s algorithm may be generally expressed as follows,
 , (9)
, (9)
 . (10)
. (10)
Hence, the searching engine is described as follows,
 , (11)
, (11)
where H denotes Walsh-Hadamard operator.
3.2. The Searching Process Description
Quantum search is such a process of repeatedly applying the search engine G to the initial state , which increase the probability amplitude of the marked state. After diagonalization, the successive operations of searching engine G can be written as follows [8],
, which increase the probability amplitude of the marked state. After diagonalization, the successive operations of searching engine G can be written as follows [8],
 , (12)
, (12)
where
 ,(13)
,(13)
 , (14)
, (14)
 , (15)
, (15)
 , (16)
, (16)
 , (17)
, (17)
 , (18)
, (18)
 , (19)
, (19)
 . (20)
. (20)
After n applications of G on  we get,
we get,
 . (21)
. (21)
such that,
 , (22)
, (22)
 . (23)
. (23)
3.3. The Success Probability of the Proposed Algorithm
From Equations (21)-(23), after n iterations, the success probability  and the failure probability
and the failure probability  can be respectively written as follows,
can be respectively written as follows,
 (24)
(24)
 (25)
(25)
and meet the following relationship .
.
3.4. The Required Number of Iterations of the Proposed Algorithm
According to [4], the searching engine G can be thought as a rotation in a 3-dimensional space, and the polarization vector of marked state is . For the initial state, the polarization vector is about
. For the initial state, the polarization vector is about , each searching iteration is a rotation of the polarization vector through angle
, each searching iteration is a rotation of the polarization vector through angle . Therefore, the required number of iterations to get a match with the highest possible probability can be calculated as follows,
. Therefore, the required number of iterations to get a match with the highest possible probability can be calculated as follows,
 , (26)
, (26)
where  is the floor operation. When
is the floor operation. When ,
,
 . (27)
. (27)
3.5. The Relation between the Proposed Algorithm and the Other Algorithms
According to the different values of α in Equation (26), the proposed algorithm can be transformed into the different algorithms. For instance, when ,
,
 , (28)
, (28)
in this case, the proposed algorithm is equivalent to the Grover’s original algorithm.
When 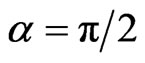 or
or ,
,
 , (29)
, (29)
in this case, the proposed algorithm is equivalent to the algorithm in [7].
When  or
or ,
,
 , (30)
, (30)
in this case, the proposed algorithm is equivalent to the algorithm in [9].
It can be seen from above depiction that the different algorithms can be achieved from the proposed algorithm according the different values of α. The above result shows that the proposed algorithm is the promotion of other search algorithms, it is the more flexible algorithm, and other algorithms can be seen as a special case of this algorithm.
In the proposed algorithm, if two phase shifts are fixed at 0.1π, then the required number of iterations is
 . (31)
. (31)
In this case, examine the system after , the success probability will be at least 99.38% compared with 98% for Younes [9], 84.72% for Younes et al. [7], and 50% for the Grover’s original algorithm, which is better than any know fixed operator quantum search algorithms.
, the success probability will be at least 99.38% compared with 98% for Younes [9], 84.72% for Younes et al. [7], and 50% for the Grover’s original algorithm, which is better than any know fixed operator quantum search algorithms.
When  or
or ,
,
 , (32)
, (32)
Figure 2 shows the success probability as a function of the ratio  for the proposed algorithm after inserting the calculated number of iterations
for the proposed algorithm after inserting the calculated number of iterations  shown in Equation (26) in Ps shown in Equation (24), where the phase shifts are set to π, π/2,
shown in Equation (26) in Ps shown in Equation (24), where the phase shifts are set to π, π/2,  , and
, and , respectively.
, respectively.
4. Performance Comparison
When  and
and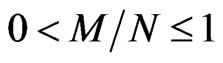 , the performance comparison of the proposed algorithm with Younes algorithm [9], Younes algorithm [7] and the Grover’s original algorithm is shown in Tables 1-5.
, the performance comparison of the proposed algorithm with Younes algorithm [9], Younes algorithm [7] and the Grover’s original algorithm is shown in Tables 1-5.
From Tables 1-5, we can see that the success probability of proposed algorithm is the highest among four algorithms; however, the inquired number of iterations is the greatest. Despite this, from Equation (27), it can still achieve quadratic speed up over classical search algo-
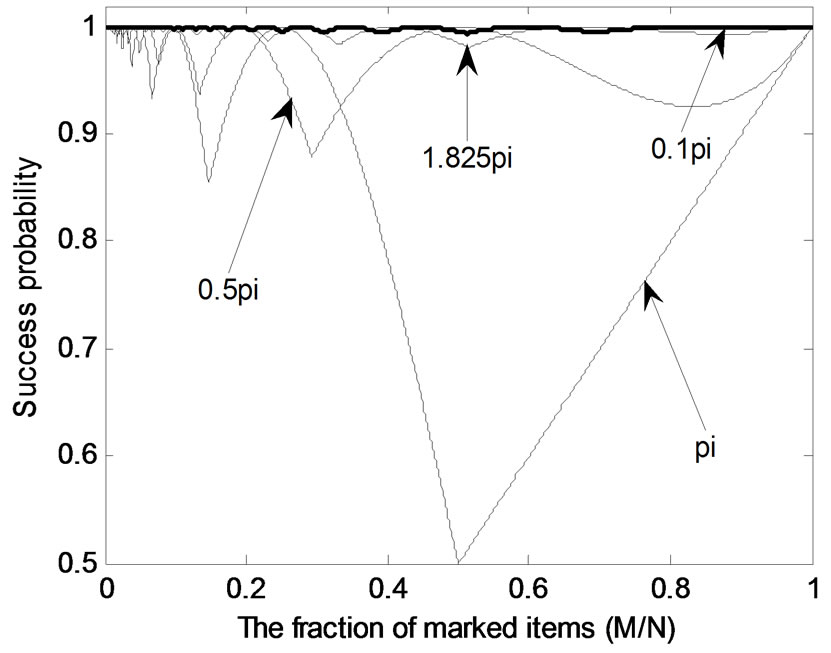
Figure 2. The success probability curves of the proposed algorithm with the different fixed-phases after the required number of iterations.

Table 1. The performance comparison of four algorithms (N = 102, α = 0.1π).

Table 2 The performance comparison of four algorithms (N = 103, α = 0.1π).

Table 3. The performance comparison of four algorithms (N = 104, α = 0.1π).

Table 4. The performance comparison of four algorithms (N = 105, α = 0.01π).

Table 5. The performance comparison of four algorithms (N = 106, α = 0.01π).
rithms. When  and
and , from Equation (31),
, from Equation (31),  , this algorithm does not seem to have achieved the quadratic speed up of Grover’s original algorithm. However, when
, this algorithm does not seem to have achieved the quadratic speed up of Grover’s original algorithm. However, when  and
and ,
,  , this algorithm has demonstrated good acceleration role, and with the increase of N, this kind of speed up will be increasingly significant.
, this algorithm has demonstrated good acceleration role, and with the increase of N, this kind of speed up will be increasingly significant.
These results can be analyzed as follows. As the saying goes, there is no free lunch. The proposed scheme obtains high successful probability at the expense of the number of iterations. When the phase shifts are fixed at , the success probability of at least 99.38% can be obtained, and when the phase shifts are fixed at
, the success probability of at least 99.38% can be obtained, and when the phase shifts are fixed at , the success probability of at least 99.99% can be obtained after more iteration. Since the phase shifts α is set to a adjustable parameter in Equation (11), the proposed scheme is more flexible, and it can obtain a balance between speed and accuracy.
, the success probability of at least 99.99% can be obtained after more iteration. Since the phase shifts α is set to a adjustable parameter in Equation (11), the proposed scheme is more flexible, and it can obtain a balance between speed and accuracy.
When , the probability curves of four search algorithms are shown in Figure 3, and the inquired iterations number curves are shown in Figure 4.
, the probability curves of four search algorithms are shown in Figure 3, and the inquired iterations number curves are shown in Figure 4.
5. Conclusion
In the future quantum computers, the search engine should be constructed from fixed operators that can handle the whole possible range of the search problem, i.e. whether a single match or multiple matches exist in the search space. Based on this consideration, in this letter, we pre-

Figure 3. The success probability distribution of four quantum search algorithms after the required number of iterations.

Figure 4. The required number of iterations for the proposed algorithm, Younes algorithm [9], Younes et al. algorithm [7] and Grover’s original algorithm.
sent a fixed-phase quantum search algorithm with more flexible behavior. The phase shifts can be fixed at the different values to meet the needs of different practical problems. If research requires a relatively rapid speed, the value of the phase shifts should be appropriately increased, if search requires a higher success probability, the value of the phase shifts should be appropriately decreased. When the phases shifts are fixed at , the proposed algorithm can get a solution with probability at least 99.38% in
, the proposed algorithm can get a solution with probability at least 99.38% in  iterations.
iterations.
6. Acknowledgements
This paper was supported by Scientific Research Foundations of Heilongjiang Provincial Education Department (Grant No. 12511009).
NOTES