Mild Solutions for Nonlocal Impulsive Fractional Semilinear Differential Inclusions with Delay in Banach Spaces ()
1. Introduction
During the past two decades, fractional differential equations and fractional differential inclusions have gained considerable importance due to their applications in various fields, such as physics, mechanics and engineering. For some of these applications, one can see [1-4] and the references therein. El Sayed et al. [5] initiated the study of fractional multi-valued differential inclusions. Recently, some basic theory for initial—value problems for fractional differential equations and inclusions was discussed by [6-14].
The theory of impulsive differential equations and impulsive differential inclusions has been an object interest because of its wide applications in physics, biology, engineering, medical fields, industry and technology. The reason for this applicability arises from the fact that impulsive differential problems are an appropriate model for describing process which at certain moments change their state rapidly and which cannot described using the classical differential problems. For some of these applications we refer to [15-17]. During the last ten years, impulsive differential inclusions with different conditions have intensely student by many mathematicians. At present, the foundations of the general theory of impulsive differential equations and inclusions are already laid, and many of them are investigated in details in the book of Benchohra et al. [18].
Moreover, a strong motivation for investigating the nonlocal Cauchy problems, which is a generalization for the classical Cauchy problems with initial condition, comes from physical problems. For example, it used to determine the unknown physical parameters in some inverse heat condition problems. The nonlocal condition can be applied in physics with better effect than the classical initial condition  For example,
For example,  may be given by
may be given by

where  are given constants and
are given constants and 
 . For the applications of nonlocal conditions problems we refer to [19,20]. In the few past years, several papers have been devoted to study the existence of solutions for differential equations or differential inclusions with nonlocal conditions [21-23]. For impulsive differential equation or inclusions with nonlocal conditions of order one we refer to [22,23]. For impulsive differential equation or inclusions of fractional order we refer to [10,24-27] and the references therein.
. For the applications of nonlocal conditions problems we refer to [19,20]. In the few past years, several papers have been devoted to study the existence of solutions for differential equations or differential inclusions with nonlocal conditions [21-23]. For impulsive differential equation or inclusions with nonlocal conditions of order one we refer to [22,23]. For impulsive differential equation or inclusions of fractional order we refer to [10,24-27] and the references therein.
In this paper we are concerned with the existence of mild solution to the following nonlocal impulsive semilinear differential inclusions with delay and of order  of the type
of the type
 (1.1)
(1.1)
where ,
,  is the Caputo derivative of order
is the Caputo derivative of order 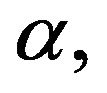
 is the infinitesimal generator of a
is the infinitesimal generator of a  semigroup
semigroup  on a real separable Banach space
on a real separable Banach space ,
, 
 be a multi-function,
be a multi-function,  is a given continuous function,
is a given continuous function,  is a nonlinear function related to the nonlocal condition at the origin,
is a nonlinear function related to the nonlocal condition at the origin,  impulsive functions which characterize the jump of the solutions at impulse points, and
impulsive functions which characterize the jump of the solutions at impulse points, and 
 are the right and left limits of
are the right and left limits of  at the point
at the point  respectively. Finally, for any
respectively. Finally, for any 
 defined by
defined by

where  and
and  will define in the next section.
will define in the next section.
To study the theory of abstract impulsive differential inclusions with fractional order, the first step is how to define the mild solution. Mophou [24] firstly introduced a concept on a mild solution which was inspired by Jaradat et al. [25]. However, it does not incorporate the memory effects involved in fractional calculus and impulsive conditions. Wang et al. [10] introduced a new concept of PC-mild solutions for (1.1) without delay and derived existence and uniqueness results concerning the PC-mild solutions for (1.1) when  is a Lipschitz single-valued function or continuous and maps bounded sets into bounded sets and
is a Lipschitz single-valued function or continuous and maps bounded sets into bounded sets and  is compact.
is compact.
In order to do a comparison between our obtained results in this paper and the known recent results in the same domain, we refer to: Ouahab [9] proved a version of Fillippov’s theorem for (1.1) without impulse, without delay and  is an almost sectorial operator, Wang et al. [11] proved existence and controllability results for (1.1) without impulse, without delay and with local condition, Zhang et al. [12] considered the problem (1.1) without impulse, without delay,
is an almost sectorial operator, Wang et al. [11] proved existence and controllability results for (1.1) without impulse, without delay and with local condition, Zhang et al. [12] considered the problem (1.1) without impulse, without delay,  is a single-valued function and
is a single-valued function and  is strongly equicontinuous C0-semigroup, Zhou et al. [13,14] introduced a suitable definition of mild solution for (1.1) based on Laplace transformation and probability density functions for (1.1) when
is strongly equicontinuous C0-semigroup, Zhou et al. [13,14] introduced a suitable definition of mild solution for (1.1) based on Laplace transformation and probability density functions for (1.1) when  is single-valued function and without impulse, Cardinali et al. [22] proved the existence of mild solutions to the problem (1.1) without delay,
is single-valued function and without impulse, Cardinali et al. [22] proved the existence of mild solutions to the problem (1.1) without delay, when
when  and
and the multivalued function
the multivalued function  satisfies the lower Scorza-Dragoni property and
satisfies the lower Scorza-Dragoni property and  is a family of linear operator, generating a strongly continuous evolution operators, Fan [23] studied a nonlocal Cauchy problem in the presence of impulses, governed by autonomous semilinear differential equation, Dads et al. [26] and Henderson et al. [27] considered the problem (1.1) when
is a family of linear operator, generating a strongly continuous evolution operators, Fan [23] studied a nonlocal Cauchy problem in the presence of impulses, governed by autonomous semilinear differential equation, Dads et al. [26] and Henderson et al. [27] considered the problem (1.1) when  Among the previous works, little is concerned with nonlocal fractional differential inclusions with impulses and with delay.
Among the previous works, little is concerned with nonlocal fractional differential inclusions with impulses and with delay.
In Section 3 in this paper, motivated by the works mentioned above, we derive various existence results of mild solutions for (1.1) when the values of the orient field are convex as well as non-convex.
The paper is organized as follows: In Section 2, we collect some background material and lemmas to be used later. In Section 3, we prove three existence results for (1.1). We adopt the definition of mild solution introduced by Wang et al. [10]. Our basic tools are the properties of multi-functions, methods and results for semilinear differential inclusions, and fixed point techniques.
2. Preliminaries and Notations
Let  the space of
the space of  -valued continuous functions on
-valued continuous functions on  with the uniform norm
with the uniform norm
 the space of E-valued Bochner integrable functions on
the space of E-valued Bochner integrable functions on  with the norm
with the norm
 ,
,  = {
= { : B is nonempty and bounded},
: B is nonempty and bounded},  = {
= { : B is nonempty and closed},
: B is nonempty and closed},  = {
= { : B is nonempty and compact},
: B is nonempty and compact},  = {
= { : B is nonempty, closed and convex},
: B is nonempty, closed and convex},  = {
= { : B is nonempty, convex and compact},
: B is nonempty, convex and compact},  (respectively,
(respectively,  )
) be the convex hull (respectively, convex closed hull in
be the convex hull (respectively, convex closed hull in ) of a subset
) of a subset 
Definition 1 ([28]). A semigroup  of bounded linear operators on a Banach space
of bounded linear operators on a Banach space  is said to be 1) uniformly continuous if
is said to be 1) uniformly continuous if

where  is the identity operator.
is the identity operator.
2) strongly continuous if

A strongly continuous semigroup of bounded linear operators on  will be called a semigroup of class
will be called a semigroup of class  or simply a
or simply a  -semigroup. It is known that if
-semigroup. It is known that if  is a
is a  -semigroup, then there exist constants
-semigroup, then there exist constants  and
and  such that
such that

A  semigroup
semigroup  is called compact if for every
is called compact if for every  is compact. It is known that ([28], Theorem 3.2) every compact
is compact. It is known that ([28], Theorem 3.2) every compact  semigroup is uniformly continuous.
semigroup is uniformly continuous.
Definition 2 ([28]). Let  be a semigroup of bounded linear operators on a Banach space
be a semigroup of bounded linear operators on a Banach space  The linear operator
The linear operator  defined by
defined by

and

is called the infinitesimal generator of the semigroup  is the domain of
is the domain of 
Definition 3 ([29-33]). Let  and
and  be two topological spaces. A multifunction
be two topological spaces. A multifunction  is said to be upper semicontinuous (u.s.c.) if
is said to be upper semicontinuous (u.s.c.) if
 is an open subset of
is an open subset of 
for every open .
.  is said to be lower semicontinuous
is said to be lower semicontinuous if
if  is an open subset of
is an open subset of  for every open
for every open 
 is called closed if its graph
is called closed if its graph
 is closed subset of the topological space
is closed subset of the topological space .
.  is said to be completely continuous if
is said to be completely continuous if  is relatively compact for every bounded subset
is relatively compact for every bounded subset  of
of  If the multifunction
If the multifunction  is completely continuous with non empty compact values, then
is completely continuous with non empty compact values, then  is u.s.c. if and only if
is u.s.c. if and only if  is closed.
is closed.
Lemma 1 ([29] Theorem 8.2.8). Let
Theorem 8.2.8). Let  be a complete
be a complete  finite measure space,
finite measure space,  a complete separable metric space and
a complete separable metric space and  be a measurable multivalued function with non empty closed images. Consider a multivalued function
be a measurable multivalued function with non empty closed images. Consider a multivalued function  from
from  to
to 
 is a complete separable metric space such that for every
is a complete separable metric space such that for every  the multivalued function
the multivalued function  is measurable and for every
is measurable and for every  the multivalued function
the multivalued function  is continuous.
is continuous.
Then the multivalued function  is measurable. In particular for every measurable singlevalued function
is measurable. In particular for every measurable singlevalued function  the multivalued function
the multivalued function  is measurable and for every Caratheodory single-valued function
is measurable and for every Caratheodory single-valued function  the multivalued function
the multivalued function  is measurable.
is measurable.
Definition 4 A nonempty subset  is said to be decomposable provided for every
is said to be decomposable provided for every  and each Lebesgue measurable
and each Lebesgue measurable set
set  in
in 
 where
where  is the characteristic function of the set
is the characteristic function of the set 
Definition 5 A sequence  is said to be semi-compact if:
is said to be semi-compact if:
1) It is integrably bounded, i.e. there is  such that
such that

2)The set  is relatively compact in
is relatively compact in 

We recall one fundamental result which follows from Dunford-Pettis Theorem.
Lemma 2 ([33]). Every semi-compact sequence in  is weakly compact in
is weakly compact in 
For more about multifunctions we refer to [29-33].
Lemma 3 ([11], lemma 2.10). For  and
and
 , we have
, we have .
.
Definition 6 According to the Riemann -Liouville approach, the fractional integral of order  of a function
of a function  is defined by
is defined by

provided the right side is defined on , where
, where  is the Euler gamma function defined by
is the Euler gamma function defined by 
Definition 7 The Caputo derivative of order  of a continuously differentiable function
of a continuously differentiable function  is defined by
is defined by

Note that the integrals appear in the two previous definitions are taken in Bochner’ sense and 
 for all
for all  For more informations about the fractional calculus we refer to [2,4].
For more informations about the fractional calculus we refer to [2,4].
Definition 8 ([14], Lemma 3.1 and Definition 3.1, see also [11-13]). Let  A function
A function  is said to be a mild solution of the following system:
is said to be a mild solution of the following system:
 (2.1)
(2.1)
if it satisfies the following integral equation
 (2.2)
(2.2)
where


 and
and  is a probability density function defined on
is a probability density function defined on  that is
that is  Note that the function must be chosen such that the integral appears in (2.2) is well be defined.
Note that the function must be chosen such that the integral appears in (2.2) is well be defined.
Remark 1 Since  are associated with the numbrer
are associated with the numbrer  there are no analogue of the semigroup property, i.e.
there are no analogue of the semigroup property, i.e. 

In the following we recall the properties of 
 .
.
Lemma 4 ([14], Lemma 3.2, Lemma 3.3 and Lemma 3.5)
1) For any fixed  are linear bounded operators.
are linear bounded operators.
2) For 
3) If  then
then for any
for any
 and
and 
4) For any fixed  are strongly continuous.
are strongly continuous.
5) If  is compact, then
is compact, then  and
and  are compact.
are compact.
In order to define the concept of mild solution of (1.1), let 

 and consider the set of functions:
and consider the set of functions:


and

It is easy to check that  are
are  are Banach spaces endowed with the norms
are Banach spaces endowed with the norms

and

For any  and any
and any  the element of
the element of  defined by
defined by

Here  represents the history of the state time
represents the history of the state time  up the present time
up the present time  For any subset
For any subset  and for any
and for any  let
let

Of course 
Let us recall the concept of mild solutions, introduced by Wang et al. [10], for the impulsive fractional evolution equation:
 (2.3)
(2.3)
where .
.
At first Wang et al. [10] considered the following nonhomogeneous impulsive fractional equation
 (2.4)
(2.4)
where  and
and  It is easily observe that
It is easily observe that  can be decomposed to
can be decomposed to  where
where  is the continuous mild solution for
is the continuous mild solution for
 (2.5)
(2.5)
and  is the mild solution for the impulsive evolution equation
is the mild solution for the impulsive evolution equation
 (2.6)
(2.6)
Indeed, by adding together (2.5) with (2.6), it follows (2.4). Note  is continuous, so
is continuous, so 
 . On the other hand, any solution of (2.4) can be decomposed to (2.5) and (2.6). By Definition 9, a mild solution of (2.5) is given by
. On the other hand, any solution of (2.4) can be decomposed to (2.5) and (2.6). By Definition 9, a mild solution of (2.5) is given by
 (2.7)
(2.7)
Now we rewrite system (2.6) in the equivalent integral equation
 (2.8)
(2.8)
The above equation can be expressed as
 (2.9)
(2.9)
where

We apply the Laplace transform for (2.8) to get (see, [25])

which implies

Note that the Laplace transform for  is
is
 Thus we can derive the mild solution of (2.6) as
Thus we can derive the mild solution of (2.6) as
 (2.10)
(2.10)
By (2.7) and (2.10), the mild solution of (2.4) is given by

By using the above results, we can write the following definition of mild solution of the system (2.3).
Definition 9 ([10], Definition 3.1). By a mild solution of the system (2.3) we mean a function 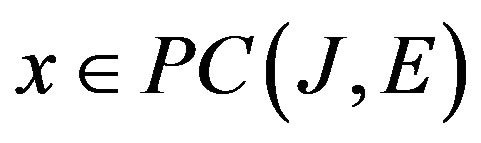 which satisfies the following integral equation
which satisfies the following integral equation

Now we can give the concept of mild solution for our considered problem (1.1).
Definition 10 By a mild solution for (1.1), we mean a function  which satisfies the following integral equation
which satisfies the following integral equation
 (2.11)
(2.11)
where  and
and  is an integrable selection for
is an integrable selection for .
.
Remark 2 It is easily to see that the solution given by (2.11) satisfies the relation
 .
.
Remark 3 If 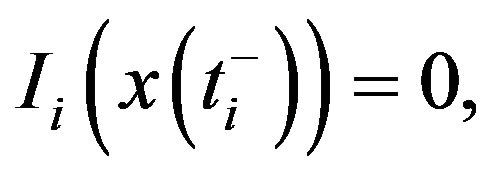 for all
for all  and if there is no delay then Formula (2.11) will take the form
and if there is no delay then Formula (2.11) will take the form

This means that when there is no neither impulse nor delay in the problem (1.1), its solution is equal to the formula given in (2.2).
Theorem 1 ([34]). Let  be a nonempty subset of a Banach space
be a nonempty subset of a Banach space , which is bounded, closed and convex. Suppose
, which is bounded, closed and convex. Suppose  is u.s.c. with closed, convex values, and such that
is u.s.c. with closed, convex values, and such that  and
and  is compact. Then
is compact. Then  has a fixed point The following fixed point theorem for contraction multivalued is proved by Govitz and Nadler [35].
has a fixed point The following fixed point theorem for contraction multivalued is proved by Govitz and Nadler [35].
Theorem 2 Let  be a complete metric space. If
be a complete metric space. If  is contraction, then
is contraction, then  has a fixed point.
has a fixed point.
Theorem 3 ([36], Corollary 3.3.1) (Schauder fixed point theorem). Let  be a Banach space,
be a Banach space,  a nonempty, convex, closed and bounded subset of
a nonempty, convex, closed and bounded subset of  and
and  be continuous. If
be continuous. If  is compact or
is compact or  is compact, then
is compact, then  has a fixed point.
has a fixed point.
3. Existence Results for the Problem (1.1)
In this section, we give the main results of mild solutions of (1.1).
3.1. Convex Case
In the following Theorem we derive the first existence result concerning the mild solution for the problem (1.1).
Theorem 4 Let  be a multifunction. Assume the following conditions:
be a multifunction. Assume the following conditions:
(H1) A is the infinitesimal generator of a  semigroup
semigroup  and
and  is compact.
is compact.
(H2) For every  is measurable, for almost
is measurable, for almost  is upper semi-continuous and for each
is upper semi-continuous and for each  the set
the set
 is nonempty.
is nonempty.
(H3) There exist a function ,
,  such that for any
such that for any 
 (3.1)
(3.1)
(H4)  is continuous, compact and there exist two positive numbers
is continuous, compact and there exist two positive numbers  such that
such that
 (3.2)
(3.2)
(H5) For every ,
,  is continuous and compact and there exists a positive constant
is continuous and compact and there exists a positive constant  such that
such that
 (3.3)
(3.3)
Then, for a given continuous function  the problem (1.1) has a mild solution provided that there is
the problem (1.1) has a mild solution provided that there is  such that
such that
 (3.4)
(3.4)
where,  such that
such that ,
,

and 
Proof. In view of (H2), for each  the set
the set

is nonempty. So, we can define a multifunction  as follows:
as follows:  if and only if
if and only if

where  Obviously, every fixed point for
Obviously, every fixed point for
 is a mild solution for the problem (1.1). So, our goal is to apply Theorem 1. The proof will be given in several steps.
is a mild solution for the problem (1.1). So, our goal is to apply Theorem 1. The proof will be given in several steps.
Step 1. The values of  are convex and closed subset in
are convex and closed subset in 
Since the values of  are convex, it is easily to see that the values of
are convex, it is easily to see that the values of  are convex. In order to prove that the values of
are convex. In order to prove that the values of  are closed, let
are closed, let  and
and  be a sequence in
be a sequence in  such that
such that  in
in  Then, according to the definition of
Then, according to the definition of  there is a sequence
there is a sequence  in
in  such that for any
such that for any 

 (3.5)
(3.5)
Not that, from (3.1), for any  for almost
for almost 

This show that the set  is integrably bounded. Moreover, because
is integrably bounded. Moreover, because
 for a.e.
for a.e. 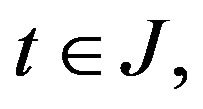 the set
the set
 is relativity compact in
is relativity compact in  for a.e.
for a.e.  Therefore, the set
Therefore, the set  is semi-compact and then, by Lemma 2 it is weakly compact in
is semi-compact and then, by Lemma 2 it is weakly compact in  So, without loss of generality we can assume that
So, without loss of generality we can assume that  converges weakly to a function
converges weakly to a function 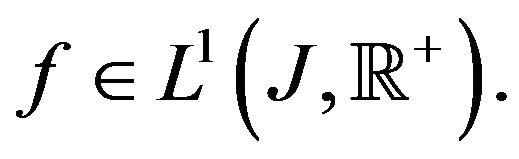 From Mazur’s lemma, there is a sequence
From Mazur’s lemma, there is a sequence  such that
such that  and
and 
converges strongly to . Since, the values of
. Since, the values of  are convex,
are convex,  and hence, by the compactness of
and hence, by the compactness of

 Moreover, for every
Moreover, for every  and for every
and for every 

Therefore, by passing to the limit as  in (3.5), we obtain from the Lebesgue dominated convergence theorem that, for every
in (3.5), we obtain from the Lebesgue dominated convergence theorem that, for every 

Then 
Step 2. We claim that  where
where

and . To prove that, let
. To prove that, let
 ,
,  and
and  If
If  then by (3.2)
then by (3.2)
 (3.6)
(3.6)
For . By using Lemma 4(3), (3.1), (3.2) and (3.5) we get
. By using Lemma 4(3), (3.1), (3.2) and (3.5) we get
 (3.7)
(3.7)
Similarly, by using Lemma 4(3), (3.1), (3.2),(3.3) and (3.5) we have for ,
, 
 (3.8)
(3.8)
Therefore, from (3.4).(3.6).(3.7) and (3.8), we conclude that .
.
Step 3. Let  We claim that
We claim that  is equicontinuous, let
is equicontinuous, let  and
and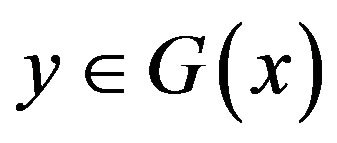 . According to the definition of
. According to the definition of  we have
we have

where  By the continuity of
By the continuity of  we can see easily that if
we can see easily that if  then
then

To show that  it suffices to verify that
it suffices to verify that  is equicontinuous for every
is equicontinuous for every , where
, where

We consider the following cases:
Case 1. Let  In view of Holder’s inequality we get
In view of Holder’s inequality we get
 (3.9)
(3.9)
Since  is compact,
is compact,  is also, (see, Lemma 4(v)), and hence,
is also, (see, Lemma 4(v)), and hence,  is uniformly continuous on
is uniformly continuous on  (see [28]). Therefore, the last inequality tends to zero as
(see [28]). Therefore, the last inequality tends to zero as  independently of
independently of 
Case 2. Let  be two points in
be two points in , then
, then
 (3.10)
(3.10)
where



and

We only need to check  as
as  for every
for every . At first, we note that, as we mention above the operators
. At first, we note that, as we mention above the operators  are uniformly continuous on
are uniformly continuous on
 So,
So,  independently of
independently of 
For  by the Holder inequality we have
by the Holder inequality we have
 (3.11)
(3.11)
independently of 
For  we note that
we note that  then for
then for
 we have
we have  By applying Lemma 3 and taking into account
By applying Lemma 3 and taking into account  we get
we get

Then

This leads to

Therefore,
 (3.12)
(3.12)
independently of 
For  by using (H1) and the Lebesgue dominated convergence theorem, we get
by using (H1) and the Lebesgue dominated convergence theorem, we get
 (3.13)
(3.13)
By the uniform continuity of  we conclude that
we conclude that  independently of
independently of 
Case 3. When , let
, let  be two points in
be two points in  Invoking to the definition of
Invoking to the definition of  we have
we have

Arguing as in the first case we get
 (3.14)
(3.14)
Case 4. When ,
,  , let
, let  be such that
be such that  and
and  such that
such that
 , then we have
, then we have

According the definition of  we get
we get

Arguing as in the first case we can see that
 (3.15)
(3.15)
From (3.9) ® (3.15) we conclude that  is equicontinuous for every
is equicontinuous for every .
.
Step 4. Our aim in this step is to show that for any , the set
, the set

is relatively compact in .
.
Let us introduce the following maps:

where


and  if and only if
if and only if

where  Obviously,
Obviously, 
Because  is a bounded subset in
is a bounded subset in  and
and 
is compact, the set

is relatively compact in . Also, since the functions
. Also, since the functions  are compact, the set
are compact, the set

is relatively compact in  It remains to show that the set
It remains to show that the set

is relatively compact in  For each
For each  arbitrary
arbitrary  and
and , we define
, we define

Note that we can rewrite  in the form
in the form

Since the operator  is compact and
is compact and  is compact on
is compact on  the set
the set

is relatively compact in . Moreover, by using (H3) and (H4) we get
. Moreover, by using (H3) and (H4) we get

Using Hölder’s inequality to get

Obviously, by Lemma 4(2), the right hand side of the previous inequality tend to zero as  Hence, there exists a relatively compact set that can be arbitrary close to the set
Hence, there exists a relatively compact set that can be arbitrary close to the set  Hence, this set is relatively compact in
Hence, this set is relatively compact in . Hence,
. Hence,  is relatively compact As a consequence of Steps 3 and 4 with Arzela-Ascoli theorem we conclude that
is relatively compact As a consequence of Steps 3 and 4 with Arzela-Ascoli theorem we conclude that
 is relatively compact.
is relatively compact.
Step 5.  has a closed graph on
has a closed graph on .
.
Let  in
in  and
and
 with
with  in
in  We will show that
We will show that  By recalling the definition of
By recalling the definition of  for any
for any  there exists
there exists  such that
such that
 (3.16)
(3.16)
Let us show that the sequence  is semicompact. From the uniform convergence of
is semicompact. From the uniform convergence of  towards
towards  for any
for any 

Moreover  is upper semicontinuous with compact values, then for every
is upper semicontinuous with compact values, then for every  there exists a natural number
there exists a natural number  such that for every
such that for every 

where  Then, the compactness of
Then, the compactness of  implies that the set
implies that the set  is relatively compact for
is relatively compact for . In addition, assumption (H3) implies
. In addition, assumption (H3) implies

Then, by Lemma 2,  is semicompact, hence weakly compact. Arguing as in Step 1 from Mazur’s theorem, there is a sequence
is semicompact, hence weakly compact. Arguing as in Step 1 from Mazur’s theorem, there is a sequence  such that
such that

and  converges strongly to
converges strongly to . Since, the values of
. Since, the values of  are convex,
are convex,  and hence,
and hence,
 . By passing to the limit in (3.16), with taking into account that
. By passing to the limit in (3.16), with taking into account that  is continuous, we obtain
is continuous, we obtain

This proves that the graph of  is closed.
is closed.
Now, as a consequence of Step 1 to Step 5, we conclude that the multifunction of  is a compact multivalued function, u.s.c with convex compact values. By applying Theorem 1, we can deduce that
is a compact multivalued function, u.s.c with convex compact values. By applying Theorem 1, we can deduce that  has a fixed point
has a fixed point  which is a mild solution of Problem (1.1).
which is a mild solution of Problem (1.1).
In the following Theorems we give another version for an existence result for (1.1).
Theorem 5 Let  be a multifunction, A is the infinitesimal generator of a
be a multifunction, A is the infinitesimal generator of a  semigroup
semigroup 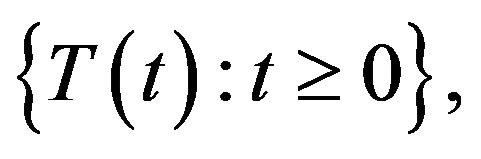 and
and  We suppose the following assumptions:
We suppose the following assumptions:
(H6) For every  is measurable.
is measurable.
(H7) There is a function  such that For every
such that For every 


(H8) There is a positive constant  such that
such that

(H9) For each  there is
there is  such that
such that

(H10)

where ,
,  and
and

Then (1.1) has a mild solution.
Proof. For  set
set

By Lemma 1, (H6) and (H7),  is measurable. Since its values are closed, it has a measurable selection (see [29], Theorem 8.1.3) which, by hypothesis
is measurable. Since its values are closed, it has a measurable selection (see [29], Theorem 8.1.3) which, by hypothesis
(H7), belongs to  Thus
Thus  is nonempty. Let us transform the problem into a fixed point problem. Consider the multifunction map,
is nonempty. Let us transform the problem into a fixed point problem. Consider the multifunction map, 
defined as follows: for 
 is the set of all functions
is the set of all functions  such that for each
such that for each 

where  It is easy to see that any fixed point for
It is easy to see that any fixed point for  is a mild solution for (1.1). So, we shall show that
is a mild solution for (1.1). So, we shall show that  satisfies the assumptions of Theorem 2. The proof will be given in two steps.
satisfies the assumptions of Theorem 2. The proof will be given in two steps.
Step1. The values of  are nonempty and closed.
are nonempty and closed.
Since  is non-empty, the values of
is non-empty, the values of  are non-empty. In order to prove the values of
are non-empty. In order to prove the values of  are closed, let
are closed, let  and
and  be a sequence in
be a sequence in  such that
such that  in
in  Then, according to the definition of
Then, according to the definition of  there is a sequence
there is a sequence  in
in  such that for any
such that for any 
 (3.17)
(3.17)
Since  is closed, for any
is closed, for any  there is
there is  such that
such that  In view of (H9), for every
In view of (H9), for every  and for a.e.
and for a.e. 

This show that the set  is integrably bounded. Using the fact that
is integrably bounded. Using the fact that  has compact values, the set
has compact values, the set  is relativity compact in
is relativity compact in  for a.e.
for a.e.  Therefore, the set
Therefore, the set  is semi-compact and in
is semi-compact and in  Then, by Lemma 2, it is weakly compact.
Then, by Lemma 2, it is weakly compact. So, we may pass to a subsequence if necessary to get that
So, we may pass to a subsequence if necessary to get that  converges weakly to a function
converges weakly to a function  From Mazur’s theorem, there is a sequence
From Mazur’s theorem, there is a sequence  such that
such that

and  converges strongly to
converges strongly to  Since, the values of
Since, the values of
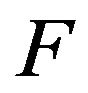 are convex,
are convex,  and hence, by the compactness of
and hence, by the compactness of 

 Note that for every
Note that for every  and for every
and for every 

Therefore, by means of the Lebesgue dominated convergence Theorem and the continuity of  we obtain from (3.17)
we obtain from (3.17)

So, 
Step 2.  is contraction. Let
is contraction. Let  and
and  Then, there is
Then, there is  such that for any
such that for any 
 (3.18)
(3.18)
Consider the multifunction  defined by
defined by

For each  is nonempty. Indeed, let
is nonempty. Indeed, let  from (H7), we have
from (H7), we have

Hence, there exists  such that
such that

Since the functions  are measurable, Proposition III.4 in [30], tells us that the multifunction
are measurable, Proposition III.4 in [30], tells us that the multifunction  is measurable. Because its values are nonempty and closed there is
is measurable. Because its values are nonempty and closed there is  with
with
 (3.19)
(3.19)
Let us define
 (3.20)
(3.20)
Obviously,  and if
and if  then by (H8)
then by (H8)

If  we get from
we get from  and (H8)
and (H8)
 (3.21)
(3.21)
Similarly, if  we get from
we get from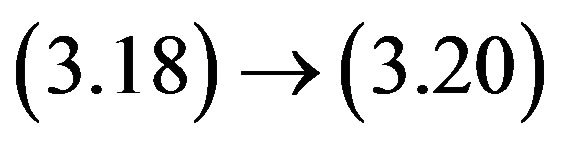 , (H8) and (H9)
, (H8) and (H9)
 (3.22)
(3.22)
By interchanging the role of  and
and , we obtain from (3.21), (3.22) and (H10)
, we obtain from (3.21), (3.22) and (H10)

Therefore,  is contraction and thus by Theorem 2
is contraction and thus by Theorem 2  has a fixed point which is a mild solution for (1.1).
has a fixed point which is a mild solution for (1.1).
3.2. Nonconvex Case
In the following Theorem we give nonconvex version for Theorem 4. Our hypothesis on the orient field is the following:
(H11)  is a multifunction such that 1)
is a multifunction such that 1)  is graph measurable and
is graph measurable and
 is lower semicontinuous.
is lower semicontinuous.
2) There exists a function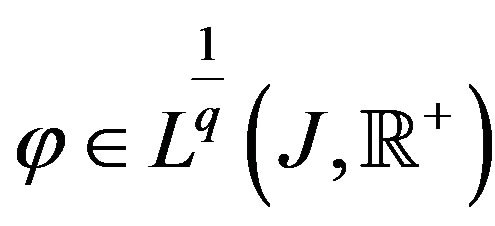 ,
,  such that for any
such that for any 

Theorem 6 If the hypotheses (H1), (H4), (H5) and (H11), then the problem (1.1) has a mild solution provided that there is  such that the condition (3.4) is satisfied.
such that the condition (3.4) is satisfied.
Proof. Consider the multivalued Nemitsky operator
 defined by
defined by

We shall prove that  has a nonempty closed decomposable value and l.s.c. Since
has a nonempty closed decomposable value and l.s.c. Since  has closed values,
has closed values,  is closed ([37]). Because
is closed ([37]). Because  is integrably bounded,
is integrably bounded,  is nonempty (see, Theorem 3.2 [37]). It is readily verified,
is nonempty (see, Theorem 3.2 [37]). It is readily verified,  is decomposable. To check the lower semi-continuity of
is decomposable. To check the lower semi-continuity of , we need to show that, for every
, we need to show that, for every 
 is upper semicontinuous. To this end from Theorem 2.2 [37], we have
is upper semicontinuous. To this end from Theorem 2.2 [37], we have
 (3.23)
(3.23)
We shall show that, for any  the set
the set

is closed. For this purpose, let  and assume that
and assume that  in
in . Then, for all
. Then, for all 
 in
in  By virtue of (H11)(1) the function
By virtue of (H11)(1) the function
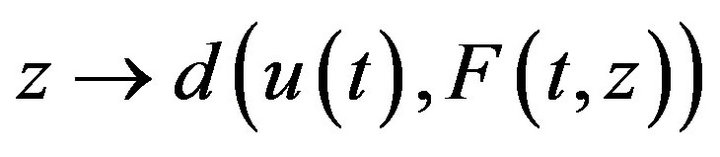 is u.s.c. So, via the Fatou Lemma, and (3.23) we have
is u.s.c. So, via the Fatou Lemma, and (3.23) we have

Therefore,  and this proves the lower semicontinuity of
and this proves the lower semicontinuity of  This allows us to apply Theorem 3 of [38] and obtain a continuous map
This allows us to apply Theorem 3 of [38] and obtain a continuous map  such that
such that 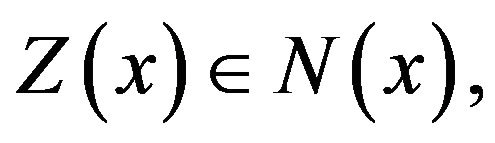 for every
for every  Then,
Then,

Consider a map  defined by
defined by

Arguing as in the proof of Theorem 4, we can show that  satiesfies all the conditions of Theorem 3 (Schauder fixed point theorem). Thus, there is
satiesfies all the conditions of Theorem 3 (Schauder fixed point theorem). Thus, there is  such that
such that  This means that
This means that  is a mild solution for (1.1).
is a mild solution for (1.1).
Remark 4 The condition (3.4) will be satisfied if

Indeed, condition (3.4) can be written as

4. Conclusion
In this paper, existence problems of nonlocal fractionalorder impulsive semi-linear differential inclusions with delay have been considered. We have been considered the case when the values of the orient field are convex as well as non-convex. Some sufficient conditions have been obtained, as pointed in the first section, theses conditions are strictly weaker than the most of the existing ones. In addition, our technique allows us to discuss some fractional differential inclusions with delay.