1. Introduction
Much has been learned since Kepler used the observations of Tyco Brahe to lay a foundation for Newtonian gravity, as subsequently embodied in general relativity through the correspondence principle. Yet the ancient concept of fixed, passive and infinite space still colors the rotation curves that play an important role in modern astronomy and astrophysics. This includes the rotation curves of spiral galaxies that led to the widespread acceptance of a poorly understood dark matter [1-3]. It also includes the rotation curves of stars orbiting the centers of galaxies suggesting that supermassive black holes reside in galactic nuclei [4,5].
This short paper will admit to the dynamic spacetime of the big bang with an emphasis on the implications for rotation curves under the standard laws of physics.
2. Formalities
2.1. The Central Mass
Throughout this paper, M will denote a large, isolated rest mass. By beginning with this mass and the two postulates below, we can explore the effect on gravity of having a gravitational field that has a finite instantaneous extent as measured from anywhere in spacetime by comoing observers rather than extending to the traditional infinite limit.
2.2. Postulates
Weak Equivalence Postulate: Gravitational mass and inertial mass are equivalent.
Big Bang Postulate: Spacetime was created by the big bang and is expanding through finite radial extents dRU.
Note that without the Big Bang Postulate, we could hardly state an estimated age for the cosmos as a single-valued function, as is a common practice.
3. The Scalar Field
It follows from the definition of the central mass M and the Weak Equivalence Postulate that for each radial distance R from the center of M, there exists uniquely a scalar field  that describes precisely the inherent, dynamic properties of the unoccupied circular orbit of radius R:
that describes precisely the inherent, dynamic properties of the unoccupied circular orbit of radius R:
 (1)
(1)
where I is the field intensity, v is the orbital speed, and ξ is the escape speed.
Recall that traditionally the field is deemed to end and free space to begin at the limit
 (2)
(2)
But (2) is replaced here by the Big Bang Postulate, above. It follows from the Big Bang Postulate that there is a minimum escape speed.
 , (3)
, (3)
Hence, there is a finite range ᴙM for ,
,
 . (4)
. (4)
It follows from (3) and (4) that
 , (5)
, (5)
which is virtually a tautology. The relativist should recognize that when a satellite orbits the central mass M, the satellite is travelling along the geodesic due to the curving of spacetime by the stress-energy tensor of M. Obviously, this is impossible beyond the range RU of the spacetime. Thus, substituting from (3) into (1), the smallest field intensity is finite,
 . (6)
. (6)
On inspection of (1) it is obvious that escape speed ξ is monotone increasing as mass,
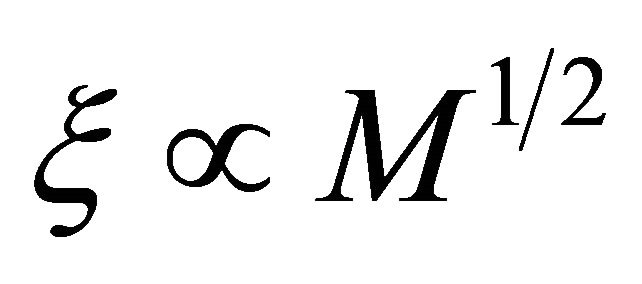 . (7)
. (7)
Otherwise, we would not have black holes. Table 1 shows some values for the minimum escape speed ε as a function of mass, with dRU = 14 × 109 light‑years. Although the current value is uncertain [6], this is on the general order of a cosmological extent.
4. The Gravitating System
Let a satellite of mass  occupy a circular orbit of M with a radius of R. (By
occupy a circular orbit of M with a radius of R. (By  is meant that m is
is meant that m is

Table 1. Minimum escape speed ε for various masses with a field range of RU = 14 × 109 light‑years.
sufficiently point-like compared to M to orbit M rather than their mutual center of mass.) Then there exists uniquely a force operator
 , (8)
, (8)
where i is the unit vector for the gravitational force, p is the unit vector for angular velocity, and j is the unit vector for the tangent to the orbit pointing away from M. The non-Albian product
 . (9)
. (9)
is a gravitating system. From (1) and (9) the orbital velocity of the satellite of mass m is
 . (10)
. (10)
For  we can write the kinetic energy of the satellite as
we can write the kinetic energy of the satellite as
 . (11)
. (11)
Substituting from (10) into (11) we obtain
 , (12)
, (12)
such that
 , (13)
, (13)
where we see from (9) that F is the force of gravity. According to (12), the radius R of the satellite’s orbit expands and contracts in inverse proportion to the kinetic energy T of the satellite,
 (14)
(14)
Thus, (14) conserves angular momentum.
It may be seen from Table 1 that when M approaches galactic magnitude, its satellite becomes tightly bound. At 2 × 1011 solar masses (on the order of the mass of the Milky Way) the satellite is so tightly bound to M that the escape velocity is 2280 kph even at the distance dRU, equivalent to the full extent of spacetime. It is as if the central mass and its satellite were the endpoints of a rigid rod. Consequently, at this galactic scale, it is not (14) that conserves angular momentum but rather an invariant period of rotation, Δt = 2π rad/θ = a constant. Since , this “dark matter” will evaporate as dRU continues to expand unless M radiates away its rest mass.
, this “dark matter” will evaporate as dRU continues to expand unless M radiates away its rest mass.
5. Conclusion
We have considered a large, isolated, central rest mass M. If we accept weak equivalence, then for each radial distance R from M there exists uniquely a scalar field  It describes the inherent, dynamic properties of an unoccupied circular orbit of M with radius R. If we accept the big bang theory, then spacetime has a finite instantaneous radius dRU, albeit monotone increasing as time, as measured from any point in spacetime by comoving observers. Hence, the escape speed in
It describes the inherent, dynamic properties of an unoccupied circular orbit of M with radius R. If we accept the big bang theory, then spacetime has a finite instantaneous radius dRU, albeit monotone increasing as time, as measured from any point in spacetime by comoving observers. Hence, the escape speed in  has a minimum value of ε = (2GMdRU1)½ and the range of
has a minimum value of ε = (2GMdRU1)½ and the range of  is the finite dRU. Next we consider a satellite of mass
is the finite dRU. Next we consider a satellite of mass 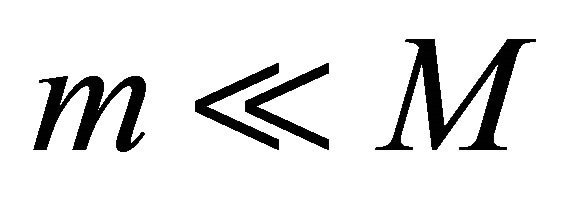 that occupies a circular orbit of
that occupies a circular orbit of  with radius R. Then there exists uniquely a force operator F, such that the non-Albian product
with radius R. Then there exists uniquely a force operator F, such that the non-Albian product  is a gravitating system. The radius R of the orbit in
is a gravitating system. The radius R of the orbit in  expands and contracts in inverse proportion to the kinetic energy T of the satellite,
expands and contracts in inverse proportion to the kinetic energy T of the satellite,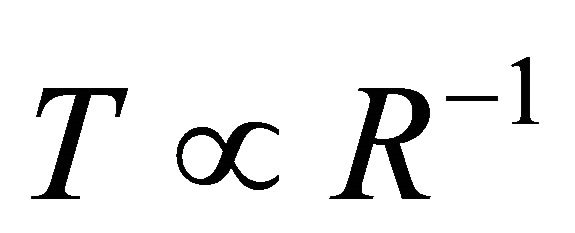 . This conserves angular momentum. But as the central mass M becomes galactic in magnitude, M and the satellite become tightly bound. For M = 2 × 1011 solar masses, the escape velocity is 2280 kph, even at the distance dRU, equivalent to the full extent of spacetime. It is as if M and m were the endpoints of a rigid rod. Hence, at this galactic scale, angular momentum is conserved by a constant period of rotation Δt = 2π rad/θ = a constant. Since
. This conserves angular momentum. But as the central mass M becomes galactic in magnitude, M and the satellite become tightly bound. For M = 2 × 1011 solar masses, the escape velocity is 2280 kph, even at the distance dRU, equivalent to the full extent of spacetime. It is as if M and m were the endpoints of a rigid rod. Hence, at this galactic scale, angular momentum is conserved by a constant period of rotation Δt = 2π rad/θ = a constant. Since , this “dark matter” will evaporate as dRU continues to expand unless M radiates away its rest mass.
, this “dark matter” will evaporate as dRU continues to expand unless M radiates away its rest mass.