1. Introduction
Fractional calculus, a popular name used to denote the calculus of non integer order, is as old as the calculus of integer order as created independently by Newton and Leibniz. In contrast with the calculus of integer order, fractional calculus has been granted a specific area of mathematics only in 1974, after the first international congress dedicated exclusively to it. Before this congress there were only sporadic independent papers, without a consolidated line [1,2].
During the 1980s fractional calculus attracted researchers and explicit applications began to appear in several fields. We mention the doctoral thesis, published as an article [3], which seems to be the first one in the subject and the classical book by Miller and Ross [1], where one can see a timeline from 1645 to 1974. After the decade of 1990, completely consolidated, there appeared some specific journals and several textbooks were published. These facts lent a great visibility to the subject and it gained prestige around the world. An interesting timeline from 1645 to 2010 is presented in references [4-6]. We recall here that an important advantage of using fractional differential equations in applications is their non-local property. The use of fractional calculus is more realistic and this is one reason why fractional calculus has become more popular.
Nowadays, fractional calculus can be considered a frontier area in mathematics in the sense that there is as much research on its applications as there is on the calculus of integer order. Several applications in all areas of knowledgement are collected, presented and discussed in different books as follow [7-12].
The main objective of this paper is to explain what is meant by calculus of non integer order and collect any different versions of the fractional derivatives associated with a particular fractional integral. Specifically, we recover the concepts of fractional integral and fractional derivative in different versions and present a new version of the so-called fundamental theorem of fractional calculus (FTFC), which is interpreted as a generalization of the classical fundamental theorem of calculus. We mention three recent works where FTFC is discussed, Tarasov’s book [12], a paper by Tarasov [13] and a paper by Dannon [14] in which a particular case of the parameter associated with the derivative is presented. The paper is written as follows: in section two, we first review the concept of fractional integral in the Riemann-Liouville sense, which can be interpreted as a generalization of the integral of integer order and in the Liouville sense, which is a particular case of the Riemann-Liouville one. We review also the concept of fractional integral in the Weyl sense and in the Riesz sense. Section two present also the concepts of derivative as proposed by Riemann-Liouville, Liouville, Caputo, Weyl and Riesz, showing the real importance and applications. Some properties are also presented, among which one associated with the semigroup property. Our main result appears in section three, in which we present and demonstrate the many faces of the FTFC, in all different versions and which are interpreted as a generalization of the fundamental theorem of calculus. Applications are presented in section four.
2. Fractional Calculus
The integral and derivatives of non integer order have several applications and are used to solve problems in different fields of knowledge, specifically, involving a fractional differential equation with boundary value conditions and/or initial conditions [7,9,11,12]. They can be seen as generalizations of the integral and derivatives of integer order. On the other hand, we mention two papers, by Heymans & Podlubny [15] and Podlubny [16] that provide an interesting geometric interpretation, and discuss applications of fractional calculus, with integral and derivatives of non integer order. Also, we mention a recent paper in which the authors discuss a fractional differential equation with integral boundary value conditions [17]. We remember that, there are several ways to introduce the concepts of fractional integral and fractional derivatives, which are not necessarily coincident with each other [18]. The so-called Grünwald-Letnikov derivative, which will be not discussed in this paper, is convenient and useful to affront problems involving a numerical treatment [19].
In this section, the concept of fractional integral in the Riemann-Liouville, Liouville, Weyl and Riesz sense is presented. Some properties involving the particular Riemann-Liouville integral are mentioned. By means of this concept we present the fractional derivatives, specifically, the Riemann-Liouville, Liouville, Caputo, Weyl and Riesz versions are discussed.
2.1. Fractional Integral of Riemann-Liouville
The fractional integral of Riemann-Liouville is an integral that generalizes the concept of integral in the classical sense, and which can be obtained as a generalization of the Cauchy-Riemann integral. As we have already said, before we define the fractional integral Riemann-Liouville.
Definition 1 (Spaces  and
and  The spaces
The spaces  and
and  are defined, for
are defined, for  and
and , by
, by

and

respectively.
Property 2.1 (Semigroup) If  or
or  and if
and if  or
or , then
, then

(Riemann-Liouville integrals) Let1 , with
, with . The fractional integrals of Riemann-Liouville of order
. The fractional integrals of Riemann-Liouville of order  with
with , on the left and on the right, are defined respectively by
, on the left and on the right, are defined respectively by

and

If , we have
, we have , where I is the identity operator.
, where I is the identity operator.
2.2. Fractional Derivative of Riemann-Liouville
After we introduce the fractional integral in the Riemann-Liouville sense, we define the fractional derivative of Riemann-Liouville, which is the most used by mathematicians, particularly, into the problems in which the initial conditions are not involved.
(Riemann-Liouville derivative) Let , with
, with  and
and , where
, where  denotes the integer part of
denotes the integer part of , the fractional derivatives in the Riemann-Liouville sense, on the left and on the right, are defined by
, the fractional derivatives in the Riemann-Liouville sense, on the left and on the right, are defined by
 (1)
(1)
and
 (2)
(2)
respectively.
Note that the derivatives in Equations (1) and (2) exist for2 .
.
If, in particular,  , then
, then

and

2.3. Fractional Integral and Derivative in the Liouville Sense
An interesting particular case of the fractional integral of Riemann-Liouville and the corresponding fractional derivative, is the so-called Liouville fractional integral and the Liouville fractional derivative. This case is obtained by substitution  and
and  in the expressions associated with the fractional integral in the Riemann-Liouville sense.
in the expressions associated with the fractional integral in the Riemann-Liouville sense.
(Liouville integral and derivative) The fractional integrals in the Liouville sense on the real axis, on the left and on the right, for  and
and , are defined by
, are defined by
 (3)
(3)
and
 (4)
(4)
respectively.
The corresponding fractional derivatives in the Liouville sense are given by
 (5)
(5)
and
 (6)
(6)
where ,
,  and
and .
.
2.4. Fractional Integral and Derivative in the Weyl Sense
The operations involving the fractional integral and the fractional derivative, as above defined by means of the Riemann-Liouville operators are convenient for a function represented by a series of power but not for functions defined, for example, by means of Fourier series, because  is a periodic function with period
is a periodic function with period the
the  cannot be periodic. For this reason, it is convenient to introduce the fractional integral and the fractional derivatives in the so-called Weyl sense. First, some remarks on the Fourier series are presented.
cannot be periodic. For this reason, it is convenient to introduce the fractional integral and the fractional derivatives in the so-called Weyl sense. First, some remarks on the Fourier series are presented.
Let  be a periodic function with period
be a periodic function with period , defined on the real axis, with null average value, i.e.,
, defined on the real axis, with null average value, i.e.,

and

representing the Fourier series of  where
where  are the corresponding Fourier coefficients. Note that, by hypotesis, as the function has null average value, we have
are the corresponding Fourier coefficients. Note that, by hypotesis, as the function has null average value, we have .
.
(Weyl integral and derivative) We define the fractional integral and the respective fractional derivatives in the Weyl sense by

and

respectively, with  and
and .
.
In the particular case , if
, if then
then  and
and where
where  and
and  are defined in Equations (3) and (5), respectively. If we define the Fourier series of
are defined in Equations (3) and (5), respectively. If we define the Fourier series of  in the form
in the form

then we obtain for , in the same way, the fractional integral in the Weyl sense on the right and the fractional derivative on the right, defined by
, in the same way, the fractional integral in the Weyl sense on the right and the fractional derivative on the right, defined by

and

respectively.
2.5. Fractional Derivative in the Caputo Sense
The differential operator of non integer order in the Caputo sense is similar to the differential operator of non integer order in the Riemann-Liouville sense. The capital difference is that: in the Caputo sense, the derivative acts first on the function, after we evaluate the integral and in the Riemann-Liouville sense, the derivatives acts on the integral, i.e., we first evaluate the integral and after we calculate the derivative. The derivative in the Caputo sense is more restritive than the Riemann-Liouville one. We also note that, both derivatives are defined by means of the Riemann-Liouvile fractional integral. The importance associated with this derivative is that, the derivative in the Caputo sense can be used, for example, in the case of a fractional differential equation with initial conditions which have a well known interpretation, as in the calculus of integer order [20,21].
(Caputo derivative) Let , with
, with
 ,
,  for
for  and
and
 . The fractional derivatives on the left,
. The fractional derivatives on the left,
 , and on the right,
, and on the right,  , in the Caputo sense, are defined in terms of the fractional integral operator of Riemann-Liouville as
, in the Caputo sense, are defined in terms of the fractional integral operator of Riemann-Liouville as
 (7)
(7)
and

For  we have
we have . In particular, if
. In particular, if , then we have
, then we have

and

2.6. Fractional Integral in the Riesz Sense
First of all, we introduce the fractional integral and the corresponding fractional derivative in the Euclidean space , but for our purpose we discuss specifically the case
, but for our purpose we discuss specifically the case , only. The operations of fractional integral and fractional derivative in the Euclidean space
, only. The operations of fractional integral and fractional derivative in the Euclidean space  are fractional powers of the Laplacian operator,
are fractional powers of the Laplacian operator,
 . For
. For  and functions
and functions , “sufficiently good” [9], with
, “sufficiently good” [9], with , the fractional operator
, the fractional operator
 is defined in terms of the Fourier transform by
is defined in terms of the Fourier transform by

The so-called fractional integral of order  in the Riesz sense, denoted by
in the Riesz sense, denoted by , which is also known by Riesz potential and is defined by the Fourier convolution product
, which is also known by Riesz potential and is defined by the Fourier convolution product

with , and
, and

is the Riesz kernel and  is defined in [9], as follows
is defined in [9], as follows

(Riesz integral) As we have already said, we take in particular,  , then
, then
 (8)
(8)
 which is the Riesz fractional integral.
which is the Riesz fractional integral.
We can also write Equation (8) in terms of the Liouville integrals. For this end, we introduce a convenient convolution product, i.e., we rewrite Equation (8) in the following form
 (9)
(9)
with ,
,  ,
, 
Applying the Fourier transform in both sides of Equation (9), we get

and

where the functions  and
and  are the Fourier transforms of the functions
are the Fourier transforms of the functions  and
and , respectively. Thus, we can write,
, respectively. Thus, we can write,

Then, rewriting Equation (8) in terms of the Liouville integrals, we get

Finally, we can write the fractional integral in the Riesz sense, in terms of a sum of two Liouville integrals
 (10)
(10)
with . For the best of our knowledged this is a new result.
. For the best of our knowledged this is a new result.
2.7. Fractional Derivative in the Riesz Sense
The fractional derivative in the Riesz sense has been introduced in problems that can be treat as a Fourier convolution product. In this section, we introduce this fractional derivative and express it in terms of the Liouville derivative. An example of a specific convolution product will be proved. As we have already mentioned, we present the general definition but we are interested in a particular case involving the parameter.
(Riesz derivative) The fractional derivative of  in the Riesz sense, with
in the Riesz sense, with , is defined for
, is defined for , by means of
, by means of
 (11)
(11)
where  and
and  are defined in [9]. The derivative in terms of the Fourier transform is
are defined in [9]. The derivative in terms of the Fourier transform is

In the particular case,  , we have
, we have
 (12)
(12)
with  and
and
 .
.
Thus, considering , we can write Equation (12) in terms of the fractional derivative in the Liouville sense, as follows
, we can write Equation (12) in terms of the fractional derivative in the Liouville sense, as follows
 (13)
(13)
with .
.
In what follow we express the Riesz derivative  in terms of a convolution product. Using Equation (13) we get
in terms of a convolution product. Using Equation (13) we get

Thus, the convenient convolution product is
 (14)
(14)
where ,
,  and
and .
.
Applying the Fourier transform in both sides of Equation (14), we obtain the Fourier transform of the function :
:


where  and
and  are the Fourier transforms of
are the Fourier transforms of  and
and , respectively. Thus,
, respectively. Thus,
 (15)
(15)
with .
.
Using this result we prove a theorem involving the Fourier convolution of two particular functions.
Theorem 1 The Fourier convolution product of the functions  and
and , with
, with  is given by
is given by
 (16)
(16)
with ,
,  and
and 
where  is the Dirac delta function.
is the Dirac delta function.
Proof. Evaluating the Fourier transform of the function , and using Equation (N) and Equation (15), we have
, and using Equation (N) and Equation (15), we have

Thus, the Fourier transform of the convolution product can be written as

To recover the convolution product, we apply the corresponding inverse Fourier transform in both sides of the last equation, and we get

Note that, the coefficient  in Equation (16) is complex, because
in Equation (16) is complex, because .
.
3. The Fundamental Theorem of Fractional Calculus
After the presentation of different versions of the fractional integral operator and the corresponding fractional derivative it is natural to introduce the corresponding FTFC associated with these different versions. Then, we present in this section the so-called FTFC, in the Riemann-Liouville, Caputo, Liouville, Weyl and Riesz versions. The results that are known we mention the reference where one can see the proof, otherwise, we present the proof. As we have already said, in all cases we first write the theorem in general form, consider a particular case and finally, we recover, as a convenient limit, the fundamental theorem in the corresponding classical version.
Theorem 2 (Riemann-Liouville) Consider a function  such that
such that , with
, with ;
;
let  with
with  and
and . If
. If
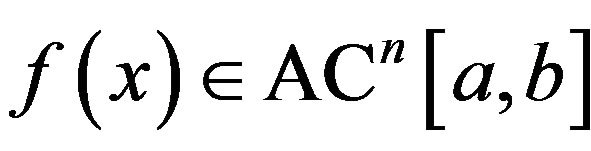 or
or  then, for every
then, for every  we have:
we have:
1)  and
and .
.
2) For  we have
we have
 (17)
(17)
and in the case , we have
, we have
 (18)
(18)
For 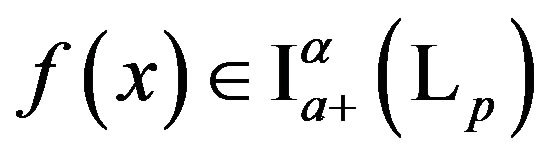 we have,
we have,
 (19)
(19)
and for  we have,
we have,
 (20)
(20)
In particular, if  in Equations (17) and (18), then
in Equations (17) and (18), then

and

On the other hand, if , we have
, we have

and

also3

and

Proof. (1) Both results follow from Lemma 2.4 in [9]. (2) To prove Equation (19) and Equation (20), we use Definition 1 and the case (1). If , then
, then . Thus, we can write,
. Thus, we can write,

Now, if , it follows in an analogous way that
, it follows in an analogous way that

The Equations (17) and (18) follow from [11]. In the particular case  we must substitute
we must substitute  in Equations (17) and (18).
in Equations (17) and (18).
In the case  we recover
we recover

and

We will now show that the Theorem 2 in which we consider the fractional operator in the Caputo sense.
Theorem 3 (Caputo) Let  be a function
be a function , with
, with  and let
and let 
with Re and
and . If
. If 
 or
or , then, for
, then, for :
:
1) For  or
or , we have
, we have
 and
and .
.
2) We have

and

In particular, if , then
, then

and, if , then
, then

and

Proof. (1) It follows from Lemma 2.21 in [9]. (2) It follows from Lemma 2.22 in [9].■
Theorem 4 (Liouville) Let  be a function defined on real axis,
be a function defined on real axis,  with
with  and
and
 . If
. If  or
or 
then, for , we have:
, we have:
1)  and
and .
.
2) If  and
and
 then
then
 and
and .
.
Proof. (1) Using Part (1) of the Theorem 2, follows

in the same way, we have .
.
(2) Using Part (2) of the Theorem 2, we have that: if , then
, then

and

with the function  when
when  or
or .■
.■
Theorem 5 (Weyl) Let  be a periodic function with period
be a periodic function with period , defined on the real axis, with null average value, and let
, defined on the real axis, with null average value, and let  with
with  then, at
then, at  in which the Fourier series of
in which the Fourier series of  is convergent, we have
is convergent, we have

Proof. Let

be the Fourier series of , with the corresponding Fourier coefficients
, with the corresponding Fourier coefficients , then
, then

and

with this, we have

In the same way, we have .■
.■
Theorem 6 (Riesz) Let , where
, where  denote the so-called the space of Lizorkin functions, defined in [9], and let
denote the so-called the space of Lizorkin functions, defined in [9], and let , then
, then
1) 
2) For ,
, .
.
Proof. (1) See Property 2.35 in [9]. (2) For , using Equation (9) we have
, using Equation (9) we have

where , and
, and .
.
Thus, using Equation (14), we get

with  and
and 
Using the Theorem 1, we obtain

Considering , and using Equation (10) and Equation (13), we can write
, and using Equation (10) and Equation (13), we can write

where .
.
By means of the Theorem 4, for , we can write
, we can write .
.
Thus, we can write

On the other hand, using Theorem 6, for , we have
, we have . In this case, we can write,
. In this case, we can write,

or in the following form,

with .
.
Evaluating , we get in the same way, that
, we get in the same way, that

with .
.
4. Applications
In this section, using the FTFC, fractional differential equations are solved, one of them associated with the Riemann-Liouville case and the other involving the Caputo case.
Example 1 Consider the following fractional differential equation and its initial condition:

with  a complex constant,
a complex constant,  and
and .
.
Applying the fractional integral operator  to the fractional differential equation and using Theorem 3, item (2), we can write
to the fractional differential equation and using Theorem 3, item (2), we can write
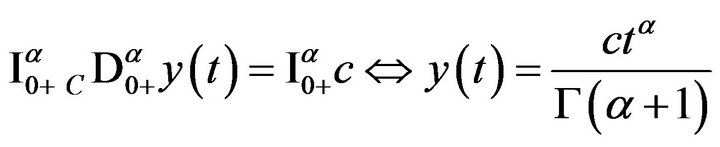 .
.
The next application, we discuss the same problem which has been discussed by Jafari & Momani [22] using another methodology, the so-called modified homotoy perturbation method. We solve the equation using the method of separation of variables and the FTFC (Riemann-Liouville).
Example 2 Consider the initial value problem involving the fractional diffusion equation
 (21)
(21)
where ,
, 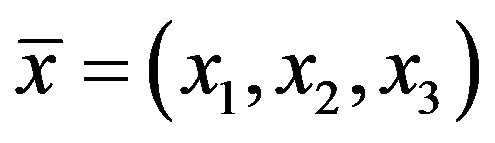 , with
, with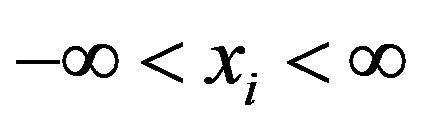 for
for ,
,  and
and .
.
Suppose a solution with the form
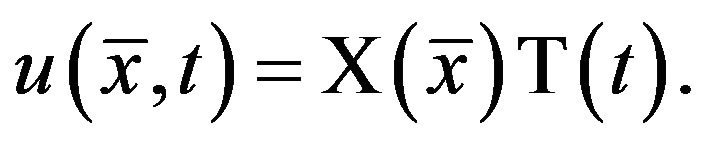 (22)
(22)
Substituting Equation (22) into the fractional diffusion equation, Equation (21), we get

where  is a real constant.
is a real constant.
We first consider the fractional differential equation . Thus, we obtain
. Thus, we obtain
 (23)
(23)
Substituting Equation (7) into Equation (23), we get an equivalent equation

Applying operator  on both sides of the last equation we have
on both sides of the last equation we have

Using Theorem 2, item (1), we can write
 (24)
(24)
As , we have
, we have . We can also write
. We can also write . Equation (24) can then be written
. Equation (24) can then be written
 (25)
(25)
This is a known equation and can be seen in reference [9], i.e., from Theorem 5.2, Equation (5.2.31) in [9] with  and
and , to obtain the result
, to obtain the result
 (26)
(26)
where  is the one-parameter Mittag-Leffler function.
is the one-parameter Mittag-Leffler function.
Using the initial condition we have

and by Equation (26),  , then
, then .
.
Substituting this result in equation involving  we have
we have , i.e.,
, i.e., .
.
Thus, the solution of the initial value problem, i.e., the fractional diffusion equation and the initial condition, is given by
 (27)
(27)
We note that, in the paper by Jafari & Momani [22] its solution is presented with a misprint, i.e., as can be verified this solution is not a solution of Equation (21). We remark, in passing, that the solution presented in the paper by Jafari & Momani [22] is different from ours because it solution is not a solution of Equation (21).
As a particular case, we consider the problem associated with the unidimensional diffusion equation, that is

where , with
, with ,
,  and
and .
.
In this case, the solution is , since,
, since,  in Equation (26). For
in Equation (26). For  the graphic is as in Figure 1.
the graphic is as in Figure 1.
5. Conclusion
After a brief introduction about the calculus of non-integer order, popularly known as fractional calculus, we presented the concept of fractional integral in the Riemann-Liouville sense. We then discussed the formulation of fractional derivatives as introduced by RiemannLiouville and, interchanging the integral with the derivative, we introduced the formulation proposed by Caputo. We presented also the fractional integral and fractional derivatives in the Liouville, Weyl and Riesz sense. As our main result, we colleted and showed the many faces of the FTFC, associated with the Riemann-Liouville, Caputo, Liouville, Weyl and Riesz version. As applications, we discussed two examples involving fractional differential equations. A natural continuation of this work resides in the fact that we can obtain solutions associated with fractional differential equations involving also fractional derivatives as proposed by Riesz and Weyl. A study in this direction is being developed [23].
6. Acknowledgements
We are grateful to Dr. J. Emlio Maiorino and Dr. Quintino A. G. Souza for several and useful discussions.
NOTES
2Space of complex functions  whose derivatives up to order
whose derivatives up to order  are absolutely continuous on
are absolutely continuous on .
.
3 .
.