1. Introduction
Gould [2] proved that
 (1)
(1)
where  and
and  are the usual Stirling numbers and the singles Stirling numbers of the first kind, respectively, defined by
are the usual Stirling numbers and the singles Stirling numbers of the first kind, respectively, defined by
 (2)
(2)
 (3)
(3)
 and.
and.
These numbers satisfy the recurrence relations
 (4)
(4)
 (5)
(5)
EL-Desouky [1] defined the generalized Stirling numbers of the first kind  called
called  -Stirling numbers of the first kind by
-Stirling numbers of the first kind by
 (6)
(6)
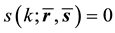 for
for  or
or  and
and  where
where  is a sequence of real
is a sequence of real
numbers and ![]() is a sequence of nonnegative integers.
is a sequence of nonnegative integers.
Equation (6) is equivalent to
![]() (7)
(7)
where ![]() and a are boson creation and annihilation operators, respectively, and satisfy the commutation rela-
and a are boson creation and annihilation operators, respectively, and satisfy the commutation rela-
tion ![]()
The numbers ![]() satisfy the recurrence relation
satisfy the recurrence relation
![]() (8)
(8)
with the notations ![]() and
and![]() .
.
The numbers ![]() have the explicit formula
have the explicit formula
![]() (9)
(9)
where ![]() with
with ![]() and
and ![]()
Moreover El-Desouky [1] derived many special cases and some applications. For the proofs and more details, see [1] .
The generalized falling factorial of x associated with the sequence ![]() of order n, where
of order n, where
![]() are real numbers, is defined by
are real numbers, is defined by ![]()
Comtet [3] [4] and [5] defined ![]() the generalized Stirling numbers of the first kind, which are called Comtet numbers, by
the generalized Stirling numbers of the first kind, which are called Comtet numbers, by
![]() (10)
(10)
These numbers satisfy the recurrence relation
![]() (11)
(11)
El-Desouky and Cakic [6] defined![]() , the generalized Comtet numbers by
, the generalized Comtet numbers by
![]() (12)
(12)
where ![]() for
for ![]() and
and![]() .
.
For more details on generalized Stirling numbers via differential operators, see [7] - [10] and [11] .
The paper is organized as follows:
In Section 2, using the differential operator ![]() we define a new family
we define a new family
of generalized Stirling numbers of the first kind, denoted by![]() . A recurrence relation and an explicit formula of these numbers are derived. In Section 3, some interesting special cases are discussed. Moreover some new combinatorial identities and a connection between
. A recurrence relation and an explicit formula of these numbers are derived. In Section 3, some interesting special cases are discussed. Moreover some new combinatorial identities and a connection between ![]() and the generalized harmonic numbers
and the generalized harmonic numbers ![]() are given. In Section 4, some applications in coherent states and matrix representation of some results obtained are given. Section 5 is devoted to the conclusion, which handles the main results derived throughout this work. Finally, a computer program is written using Maple and executed for calculating the generalized Stirling numbers of the first kind and some special cases, see Appendix.
are given. In Section 4, some applications in coherent states and matrix representation of some results obtained are given. Section 5 is devoted to the conclusion, which handles the main results derived throughout this work. Finally, a computer program is written using Maple and executed for calculating the generalized Stirling numbers of the first kind and some special cases, see Appendix.
2. Main Results
Let ![]() be a sequence of real numbers and
be a sequence of real numbers and ![]() be a sequence of nonnegative integers.
be a sequence of nonnegative integers.
Definition 2.1
The generalized Stirlng numbers ![]() are defined by
are defined by
![]() (13)
(13)
where ![]()
![]() for
for ![]() and
and![]() .
.
Equation (13) is equivalent to
![]() (14)
(14)
Theorem 2.1
The numbers ![]() satisfy the recurrence relation
satisfy the recurrence relation
![]() (15)
(15)
with the notations ![]()
Proof
![]()
Equating the coefficients of ![]() on both sides yields (15).
on both sides yields (15).
Theorem 2.2
The numbers ![]() have the explicit formula
have the explicit formula
![]() (16)
(16)
Proof
![]()
![]()
thus, by iteration, we get
![]() (17)
(17)
Setting ![]() we obtain
we obtain
![]() (18)
(18)
Comparing (13) and (18) yields (16).
3. Special cases
Setting ![]() in (13), we have the following definition.
in (13), we have the following definition.
Definition 3.1
For any real number r and nonnegative integer s, let the numbers ![]() be defined by
be defined by
![]() (19)
(19)
where ![]() and
and ![]() for
for![]() .
.
Equation (19) is equivalent to
![]() (20)
(20)
Corollary 3.1
The numbers ![]() satisfy the recurrence relation
satisfy the recurrence relation
![]() (21)
(21)
Proof
The proof follows directly from equation (15) by setting ![]() and
and ![]()
Corollary 3.2
The numbers ![]() have the explicit formula
have the explicit formula
![]() (22)
(22)
Proof
By substituting ![]() and
and ![]() in Equation (17), yields
in Equation (17), yields
![]()
then setting ![]() we have
we have
![]() (23)
(23)
hence comparing equations (19) and (23) we obtain equation (22).
Furthermore we handle the following special cases.
i) If![]() , then we have
, then we have
Definition 3.2
![]() (24)
(24)
where ![]() and
and ![]() for
for ![]()
Corollary 3.3
The numbers ![]() satisfy the recurrence relation
satisfy the recurrence relation
![]() (25)
(25)
Proof:
The proof follows directly from Equation (21) by setting![]() .
.
Corollary 3.4
The numbers ![]() have the explicit formula
have the explicit formula
![]() (26)
(26)
Proof
The proof follows directly from Equation (22) by setting![]() .
.
ii) If![]() , then we have
, then we have
Definition 3.3
The numbers ![]() are defined by
are defined by
![]() (27)
(27)
where ![]() and
and ![]() for
for ![]()
Corollary 3.5
The numbers ![]() satisfy the triangular recurrence relation
satisfy the triangular recurrence relation
![]() (28)
(28)
Proof
The proof follows easily from (22) by setting![]() .
.
Corollary 3.6
The numbers ![]() have the following explicit formula
have the following explicit formula
![]() (29)
(29)
Proof
The proof follows from (22) by setting![]() .
.
Also, using the recurrence relation (28) we can find the following explicit formula.
Theorem 3.1
The numbers ![]() have the following explicit expression
have the following explicit expression
![]() (30)
(30)
Proof
For![]() ,
,![]()
For![]() , we get
, we get
![]()
That is the same recurrence relation (28) for the numbers ![]() This completes the proof.
This completes the proof.
iii) If ![]() and
and![]() , then we have
, then we have
Definition 3.4
The numbers ![]() are defined by
are defined by
![]() (31)
(31)
where ![]() and
and ![]() for
for ![]()
Equation (31) is equivalent to
![]() (32)
(32)
Corollary 3.7
The numbers ![]() satisfy the triangular recurrence relation
satisfy the triangular recurrence relation
![]() (33)
(33)
Proof
The proof follows by setting ![]() in equation (28).
in equation (28).
Corollary 3.8
The numbers ![]() have the explicit formula
have the explicit formula
![]() (34)
(34)
Proof
The proof follows by setting ![]() in equation (29).
in equation (29).
Moreover ![]() have the following explicit formula.
have the following explicit formula.
Corollary 3.9
The numbers ![]() have the following explicit expression
have the following explicit expression
![]() (35)
(35)
Proof
The proof follows by setting ![]() in (30).
in (30).
From equations (29) and (30) (also from equations (34) and (35)) we have the combinatorial identities
![]() (36)
(36)
![]() (37)
(37)
From equations (29) and (34) we obtain that
![]() (38)
(38)
Remark 3.1
Operating with both sides of equation (13) on the exponential function![]() , we get
, we get
![]()
Therefore, since a nonzero polynomial can have only a finite set of zeros, we have
![]() (39)
(39)
If![]() , we obtain
, we obtain
![]() (40)
(40)
Remark 3.2
From relation (39), by replacing ![]() with
with![]() , and relation (18) we conclude that
, and relation (18) we conclude that
![]() (41)
(41)
This gives us a connection between ![]() and
and ![]() the generalized Comtet numbers, see [6].
the generalized Comtet numbers, see [6].
Setting ![]() and
and ![]() in (39), we get
in (39), we get
![]() (42)
(42)
hence, we have ![]() where
where ![]() see [6].
see [6].
If![]() , then
, then
![]() (43)
(43)
Next we discuss the following special cases of (42) and (43):
i) If![]() , then
, then
![]() (44)
(44)
hence we have ![]() the generalized Comtet numbers, where
the generalized Comtet numbers, where ![]()
![]() see [6] .
see [6] .
ii) If![]() , then we have
, then we have
![]() (45)
(45)
hence we obtain ![]() Comtet numbers, where
Comtet numbers, where![]() , see [3] and [4] .
, see [3] and [4] .
For example if ![]() and s = 2 in (43) we have
and s = 2 in (43) we have
![]() (46)
(46)
Using Table 2,
L.H.S. of (46) = s(3,0;2,2) + s(3,1;2,2) + s(3,2;2,2) + s(3,3;2,2) + s(3,4;2,2) + s(3,5;2,2) + s(3,6;2,2) = 14400 + 22080 +12784 + 3552 + 508 + 36 + 1 = 53361.
R.H.S. of (46) =![]() .
.
This confirms (46) and hence (43).
Another example if n = 2, r = 2 and s = 3 in (43) we have
![]() (47)
(47)
Using Table 3,
L.H.S. of (47) = s(2,0;2,3) + s(2,1;2,3) + s(2,2;2,3) + s(2,3;2,3) + s(2,4;2,3) + s(2,5;2,3) + s(2,6;2,3) = 1728 + 3456 + 2736 + 1088 + 228 + 24 + 1 = 9261.
R.H.S. of (46) =![]() .
.
This confirms (43).
iii) If![]() , then we get
, then we get
![]() (48)
(48)
hence we have ![]() which is a special case of Comtet numbers, where
which is a special case of Comtet numbers, where
![]() see [3] and [4] and Table 1.
see [3] and [4] and Table 1.
Setting![]() , we have
, we have ![]() then substituting in (2.1) it becomes
then substituting in (2.1) it becomes
![]() (49)
(49)
Using, see [12] ,
![]()
then equation (49) yields
![]() (50)
(50)
Comparing this equation with Equation (4.1) in [6] , we get
![]() (51)
(51)
where ![]() and
and ![]() are the generalized Comtet numbers of the first
are the generalized Comtet numbers of the first
kind.
Furthermore, using our notations, it is easy from Equation (4.4) in [6] and (41) to show that
![]() (52)
(52)
where ![]() and
and ![]() are the Stirling numbers of the second kind.
are the Stirling numbers of the second kind.
Next, we find a connection between ![]() and the generalized harmonic numbers
and the generalized harmonic numbers ![]() which are defined by, see [13] and [14] ,
which are defined by, see [13] and [14] ,
![]()
From (42), we have
![]()
Equating the coefficients of ![]() on both sides, we obtain
on both sides, we obtain
![]() (53)
(53)
From (22) and (53), we have the combinatorial identity
![]() (54)
(54)
hence, setting![]() , we get the identity
, we get the identity
![]() (55)
(55)
4. Some Applications
4.1. Coherent state and normal ordering
Coherent states play an important role in quantum mechanics especially in optics. The normally ordered form of the boson operator in which all the creation operators ![]() stand to the left of the annihilation operators . Using
stand to the left of the annihilation operators . Using
the properties of coherent states we can define and represent the generalized polynomial ![]() and generalized
and generalized
number ![]() as follows.
as follows.
Definition 4.1
The generalized polynomial ![]() is defined by
is defined by
![]() (56)
(56)
and the generalized number ![]()
![]() (57)
(57)
For convenience we apply the convention
![]() (58)
(58)
Now we come back to normal ordering. Using the properties of coherent states, see [7] , the coherent state matrix element of the boson string yields the generalized polynomial ![]()
![]() (59)
(59)
Definition 4.2
We define the polynomial ![]() as
as
![]() (60)
(60)
and the numbers
![]() (61)
(61)
For convenience we apply the conventions
![]() (62)
(62)
Similarly, using the properties of coherent states and (32) we have
![]() (63)
(63)
4.2. Matrix Representation
In this subsection we derive a matrix representation of some results obtained.
Let ![]() be
be ![]() lower triangle matrix, where
lower triangle matrix, where ![]() is the matrix whose entries are the numbers
is the matrix whose entries are the numbers![]() ,
,
i.e. ![]() Furthermore let
Furthermore let ![]() be an
be an ![]() lower triangle matrix defined by
lower triangle matrix defined by
![]() ,
, ![]() is a diagonal matrix whose entries of the main diagonal are
is a diagonal matrix whose entries of the main diagonal are![]() ,
,
i.e. ![]() and
and
![]() .
.
Equation (27), may be represented in a matrix form as
![]() (64)
(64)
for example if n = 3 then
![]() (65)
(65)
its inverse is given by
![]() (66)
(66)
Setting r = 1 in (64), we get
![]() (67)
(67)
![]() (68)
(68)
hence
![]()
For n = 3, we have
![]() (69)
(69)
5. Conclusion
In this article we investigated a new family of generalized Stirling numbers of the first kind. Recurrence relations and an explicit formula of these numbers are derived. Moreover some interesting special cases and new combinatorial identities are obtained. A connection between this family and the generalized harmonic numbers is given. Finally, some applications in coherent states and matrix representation of some results are obtained.
Appendix
Tables of ![]() calculated using Maple, for some values of n, k, r and s:
calculated using Maple, for some values of n, k, r and s:
![]()
Table 3. 0 ≤ n, k ≤ 4, r = 2, and s = 3.
Notice that the last column in all tables is just the sum of the entries of the corresponding row.