悖論是一種看似矛盾或不合邏輯的敘述,但那也可能是對的。
文:Chih C. Yang
為何有集合論?
蓋房子前先了解你的地基,集合論(Set theory)是現代數學的基礎。

Photo Credit: 三民出版
- 集合論

Photo Credit: 三民出版
數學的大部分理論,都是經由好幾世代的數學家努力,長期累積而來的。
但集合論卻是在19世紀末由格奧爾格.康托爾(Georg Cantor, 1849-1918)所創立的。

Photo Credit: 三民出版
無限集合
康托爾教我們如何藉由比較有限集合的方法去比較無限集合(Infinite Sets)的大小—透過像基數(cardinality,集合的元素個數)與可數(denumerability)這些清楚的概念定義。
- 芝諾悖論:阿基里斯和烏龜
在康托爾的年代之前,人們對無限的理解非常匱乏,而在數學上的無限又是隱晦且充滿矛盾的。芝諾悖論(Zeno's Paradox)就是一個這樣的例子(西元前490-425年)。

Photo Credit: 三民出版
在賽跑中,阿基里斯讓烏龜的起跑點在他前面領先一段距離,比如說10公尺吧。阿基里斯必須跑10公尺才能到達烏龜剛才的起跑點,但當他到達這個起跑點時,烏龜又已經跑到更前面的位置了。無論如何追趕,每當阿基里斯抵達烏龜剛才的位置,烏龜又已經跑到更前面的位置了。因為阿基里斯必須到達沿路上烏龜前進路線的無數多個位置點,所以他根本追不上烏龜。
在中世紀,歐洲的數學發展幾乎是停滯不前的。無限的概念已經變成一門神學而非科學了。
宇宙間大部分的模式都是被認為是有限的,唯一的無限是上帝。

Photo Credit: 三民出版
直到16世紀,無限才被接受與紀錄下來,視同數學上一門合理的、正當的研究主題。

Photo Credit: 三民出版
無限是多大?
- 在有限的世界中計數

Photo Credit: 三民出版
在數字發明之前,牧羊人用一堆小石子與羊群一對一配對,一顆小石子對應一隻羊。當牧羊人拿著小石子與羊群逐一對照,若對照完後發現小石子有剩,則代表有羊隻走失。

Photo Credit: 三民出版
在數字發明之後,計數才變成可能的事。在計數時,自然數取代了小石子,並以一對一的方式與羊隻配對。

Photo Credit: 三民出版
計數──一種比使用小石子來配對更為抽象的一對一形式──比較有限集合的大小時運作良好。但是當數學家將它拿來比較無限集合的個數時,就導致矛盾與悖論發生。
無限集合的計數
- 悖論1
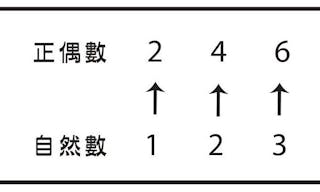
試著想像以一對一配對方式,計算所有正偶數的個數。

Photo Credit: 三民出版
根據上表,你可以看到每一個正偶數都有一個自然數對應。那麼,它看起來好像偶數集合與自然數集合(包括奇數)是「一樣多」的。
- 悖論2
另一個藉由一對一對應來比較大小的例子:

Photo Credit: 三民出版
C1和C2是兩個同心圓,a1是C1圓上的一點,a2是C2圓上的一點,且a1與a2都落於從同心圓畫出的一條射線上。因此對每一條我們所畫的射線,我們都可以建立一個圓C1上的點和圓C2上的點之間的一對一對應。
因此,我們可能得到圓C1和圓C2是「相同大小」的結論。
悖論是一種看似矛盾或不合邏輯的敘述,但那也可能是對的。
書籍介紹
《數思漫想-漫畫帶你發現數學中的思考力、邏輯力、創造力》,三民出版
.透過以上連結購書,《關鍵評論網》由此所得將全數捐贈聯合勸募。
作者:Chih C. Yang
譯者:陳玉芬、涂佩瑜、李偉任、潘漢文、李靜平、張嘉芸、李伶芳、陳財宏、朱志竣、李少宇
數學不能用背的,需要的是理解!但對於看到冗長的文字解釋,總是讓人乏味無力,甚至完全無法想像!
針對具有不同數學能力的讀者,幫助讀者欣賞和享受現代抽象數學的美,並激發學習各種數學主題的興趣與思維方式。為了保持讀者的熱情,作者使用很多具體的例子來說明一般概念的樣貌。

Photo Credit: 三民出版
責任編輯:朱家儀
核稿編輯:翁世航