I adore Rube Goldberg machines as much as the next puzzle-fanatic, but I never had the pleasure of playing the Goldberg-inspired board game Mouse Trap. As I understand it, the gameplay didn’t matter much. The joy was in building a contraption that, with the crank of a gear, set off a chain reaction in which a marble zig-zagged down a staircase, a diver launched into a bucket, and eventually a cage lowered onto a plastic pest. Apparently, when originally pitched, the president of Milton Bradley rejected the ideaas “a lot of plastic junk,” saying “this is not a game, this is nothing.” Of course it went on to be a huge commercial success, spawning copycats and even a touring life-size replica that culminates in dropping a bank safe onto a car.
This week, you’ll play the exterminator and try to snare a wily mouse.
Did you miss last week’s puzzle? Check it out here, and find its solution at the bottom of today’s article. Be careful not to read too far ahead if you haven’t solved last week’s yet!
Puzzle #13: Mouse Trap
You have five cabinets lined up in a row, and there is a mouse hiding in one of them. Each day, you can open one cabinet to try to find the mouse. If you don’t find it, you close the cabinet, and that night, the mouse moves to one of the cabinets adjacent to it (e.g., if the mouse was hiding in cabinet 2, then it must move to either cabinet 1 or cabinet 3 that night. If the mouse was hiding on the end in cabinet 1, then it must move to cabinet 2 that night, etc.) What sequence of cabinet openings should you use to guarantee that you find the mouse in the fewest number of days, regardless of the mouse’s strategy?
Happy hunting. I sometimes try to end these articles with a thematic pun, but this time I worry it’ll be too cheesy.
I’ll be back next week with the solution and a new puzzle. Do you know a cool puzzle that I should cover here? Send it to me at [email protected]
Solution to Puzzle #12: Matchstick Puzzles
Did you blaze through last week’s matchstick puzzles, or did your efforts go up in flames? Check out the solutions below.
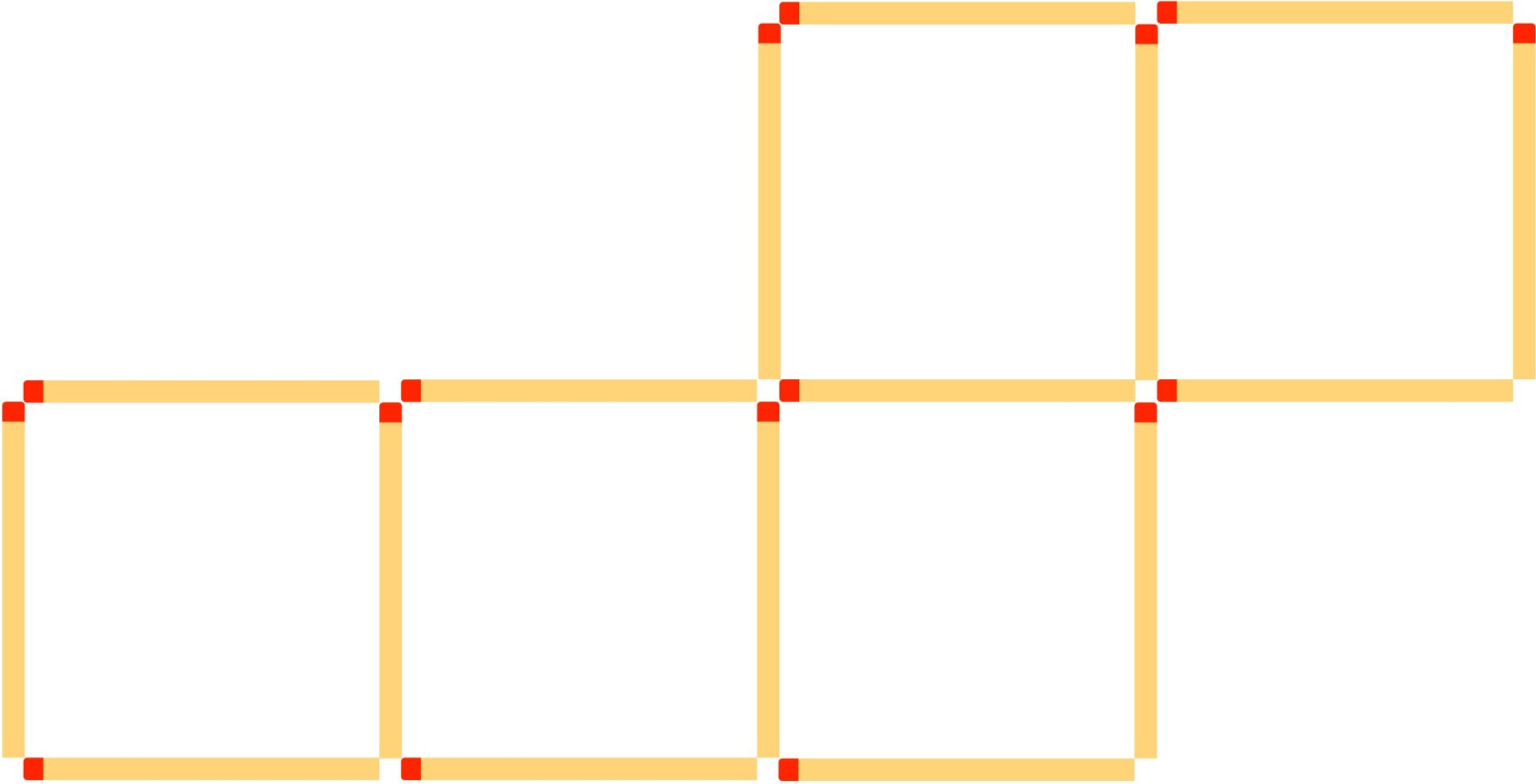
Move two matchsticks so that four one-by-one squares remain. The two matchsticks must be placed somewhere in the diagram and contribute to the final image. Solution:
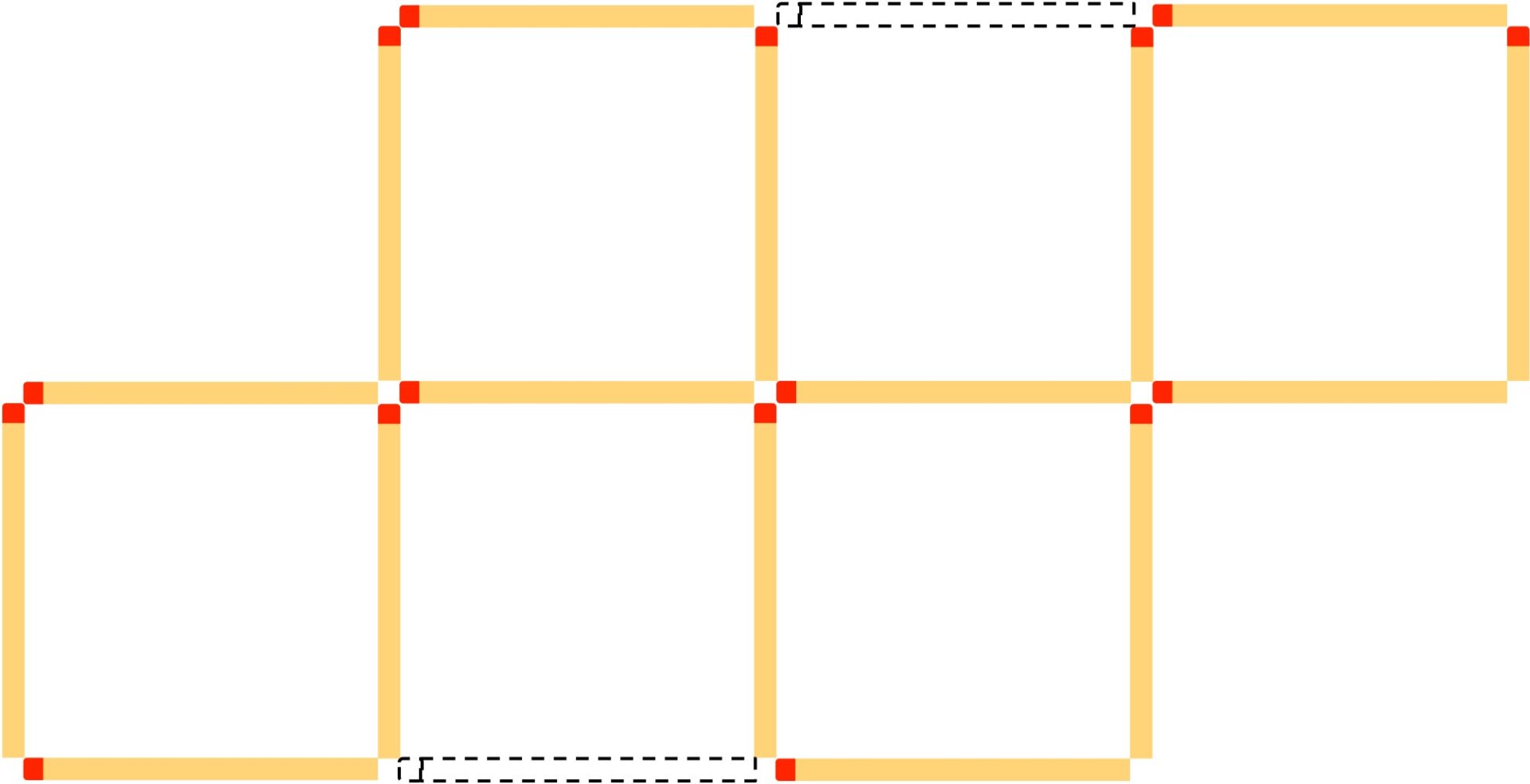
One way you could actually reason through this one is to count up the matchsticks and notice that there are 16 of them. Since four squares have 16 total sides, you can deduce that none of the resulting squares will share a side. This observation constrains the search space considerably. Next puzzle:
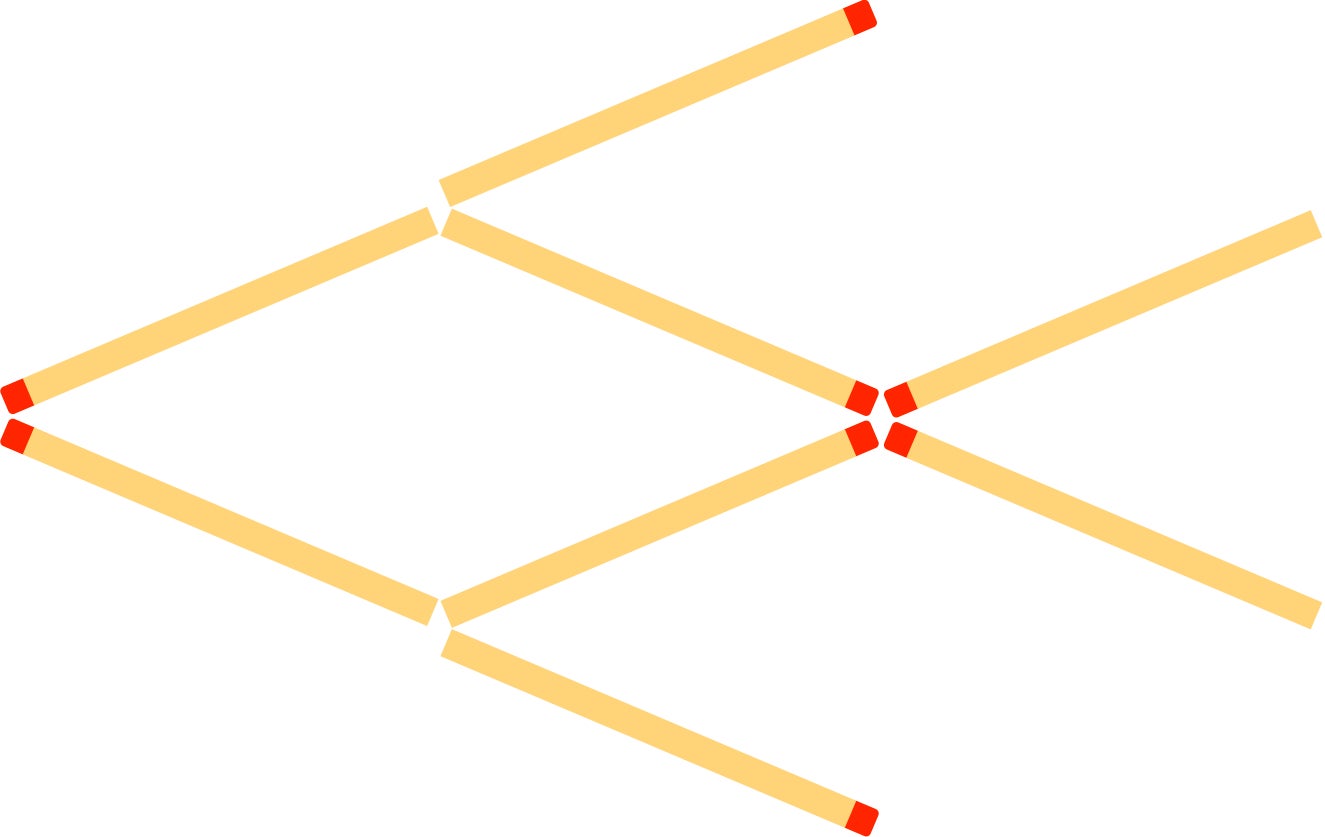
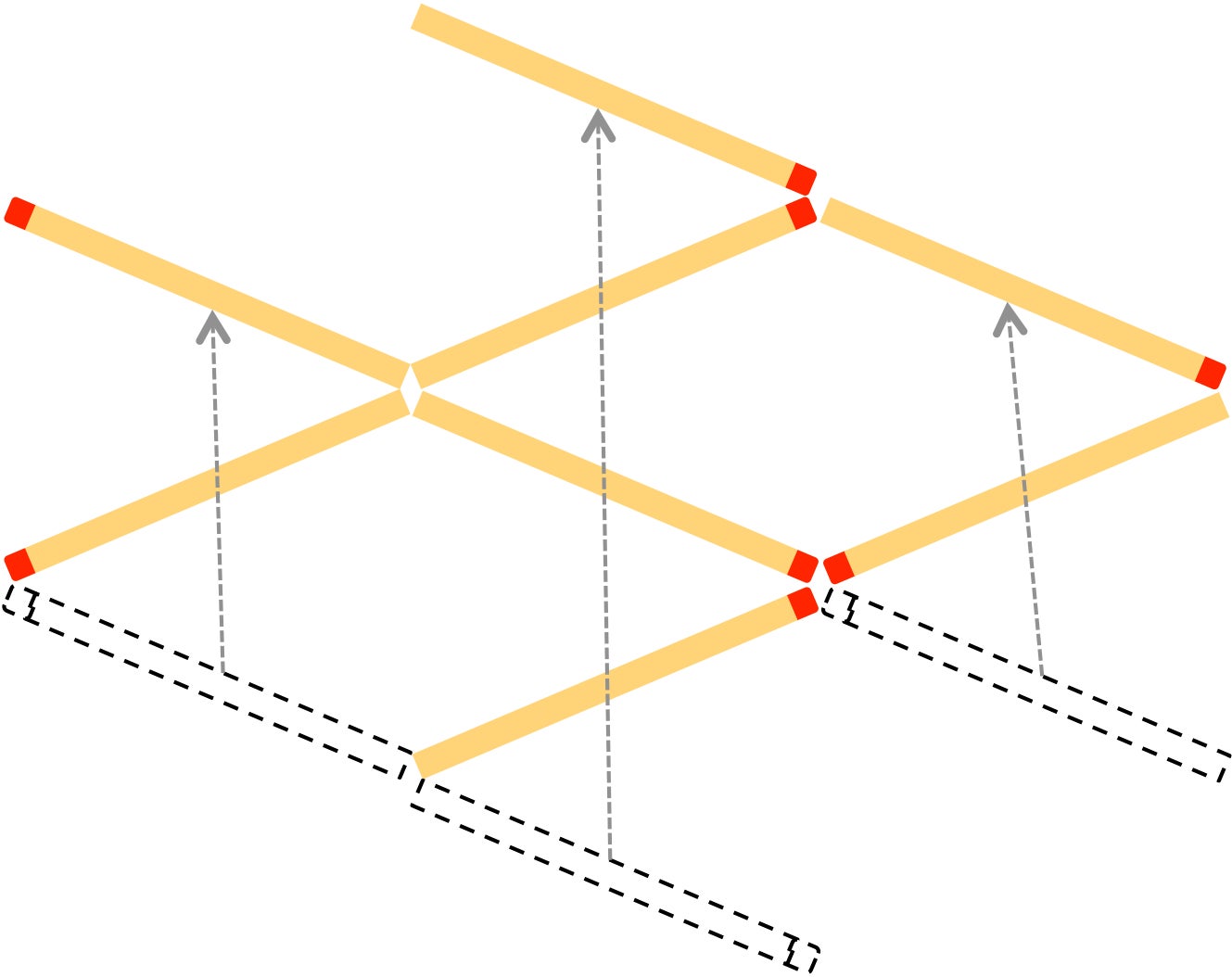
This is a fish swimming to the left. Move three matchsticks so that the same fish pattern swims to the right. Solution:
Our final puzzle was to correct a faulty equation:
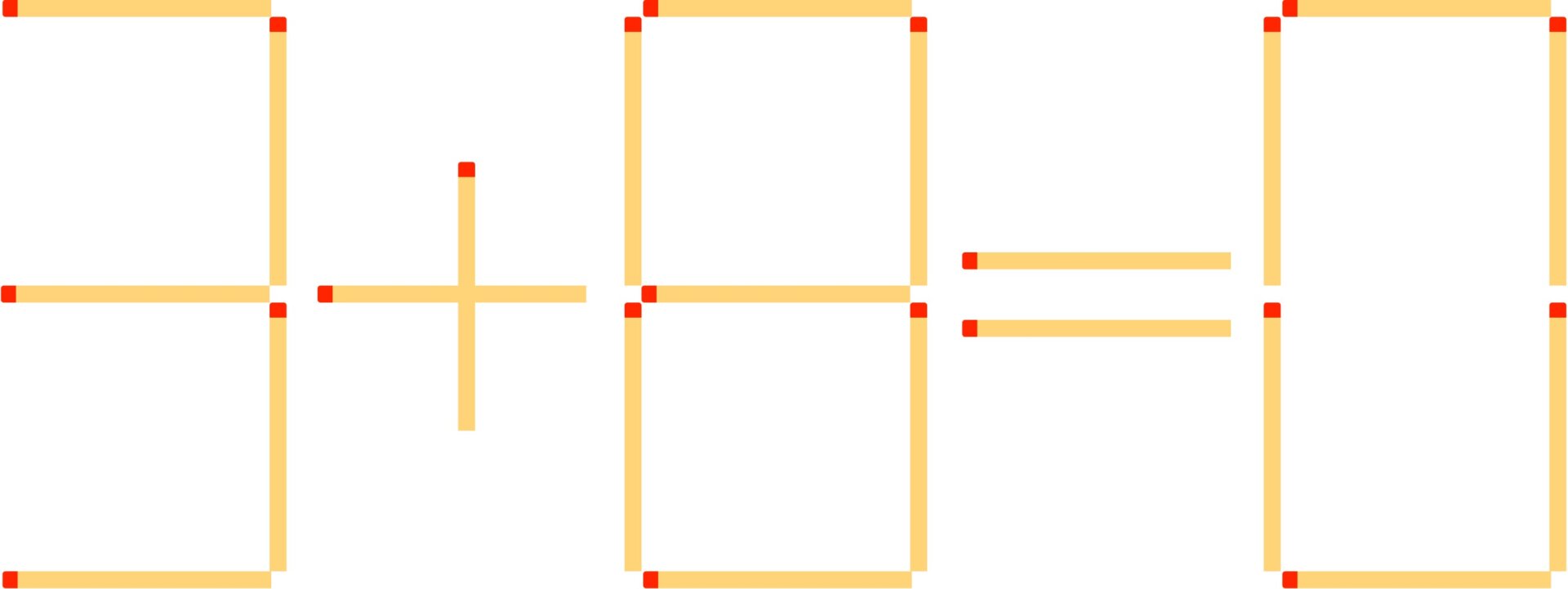
Above, matchsticks depict numbers like on a digital clock. The equation 3+8=0 is incorrect. Remove only two matchsticks to form a true equation. Solution:
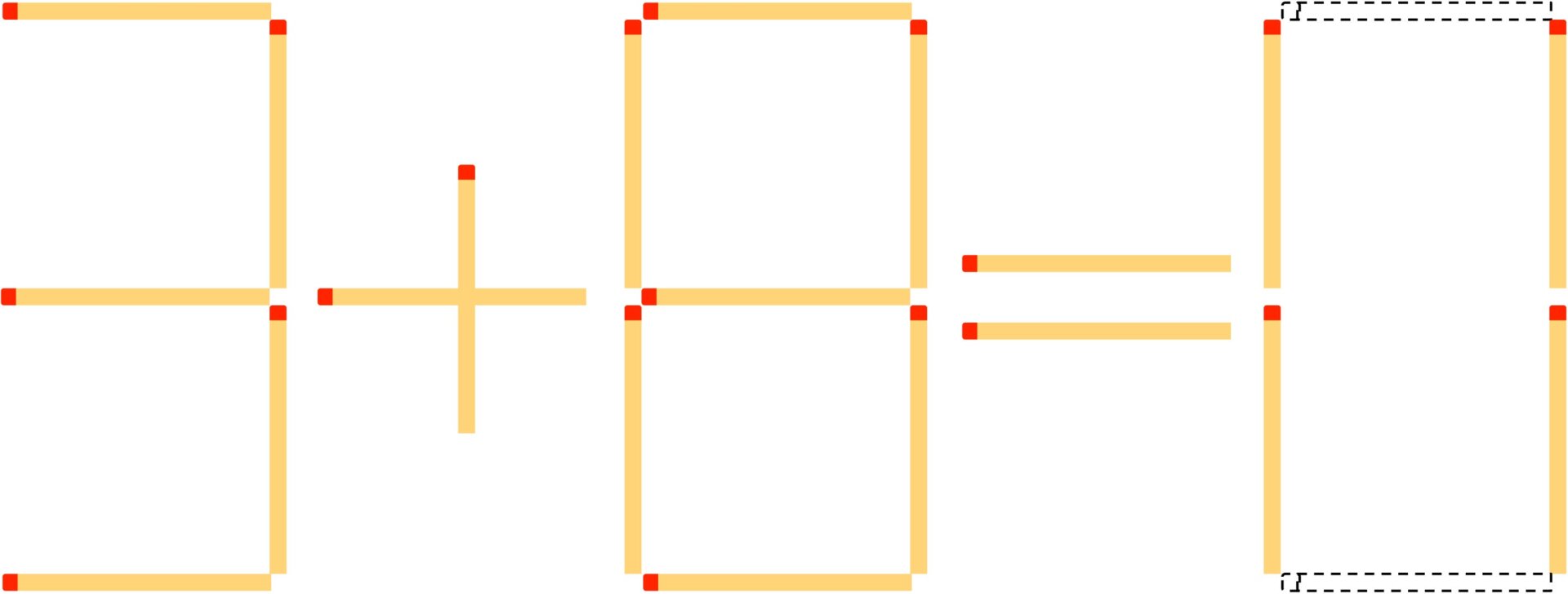
3+8 does equal 11.














