\[\Large 3^{x+2}-3^{2x+1}=6\]
次の方程式を解け。
Share:
$a>0,b>0$のとき
\begin{equation}\frac{a+b}{2}\geqq\sqrt{ab}\end{equation}
が成立し、等号は$a=b$のとき成立します。
2021年9月29日
2021年9月27日
2021年9月26日
2021年9月25日
数の大小比較（平方根の計算・二重根号）
\[2\left(\sqrt{6+2\sqrt{5}}-\sqrt{5}\right)\qquad\fbox{ ？ }\qquad 2\]
「上の$\fbox{ ？ }$に当てはまるものを以下の選択肢から選べ。
ア. > イ. = ウ. <
」
Share:
2021年9月22日
2021年9月20日
10進数の小数を2進数の小数に変換するには
10進数の数を位ごとに分解すると、
\[1234=1× 10^3+2× 10^2+3× 10^1+4× 10^0\]
のように$10$の累乗の和で表すことができます。これは2進数においても同じです。
Share:
2021年9月18日
床と2つの円に囲まれた正方形
|
| 図1 床と2つの円に囲まれた正方形 |
このような問題はどのように解けばよいでしょうか？
Share:
2021年9月16日
2021年9月15日
円に内接する四角形の対角の和はなぜ180°なのか？
なぜそうなるのかは円周角の定理を利用することでいくつかの方法で確かめることができます。
Share:
接線と弦のつくる角（接弦定理）
\[∠\text{CAT}=∠\text{ABC}\]
という関係が成り立ちます。この関係は接弦定理と呼ばれます。
本当に接弦定理は成り立つのでしょうか？確かめてみます。
Share:
10進数を2進数に変換する
10進数
10進数の数として例えば$(1234)_{10}$について考えてみます。
これをを繰り返し10で割ってみます。
10で割ったあと余りを出し、商をさらに10で割ります。この計算をしやすいように割り算の筆算を逆さまにしたような書き方でおこないます。
商が0になるまで割り続け、余りの数を下から並べ直すと元の$1234$という数が出てきます。
10で1回割ると10より小さい$4$が余りとして出てきます。
\[1234=10× 123+4\]
これを式で表すと上のようになります。10に掛けている数が商となります。
商の$123$を10で割ると次は余りとして$3$が出てきます。
\begin{align*}1234&=10(10× 12+3)+4\\ &=100× 12+10× 3+4\end{align*}
$123$を$10× 12+3$とすることで商の$12$と余りの$3$に分解しています。
これを繰り返していきます。
\begin{align*}1234&=100(10× 1+2)+10× 3+4\\ &=1000× 1+100× 2+10× 3+4\end{align*}
これで、$(1234)_{10}$を位ごとに分解することができました。これが筆算で行っていることです。
位を10で表すと10の累乗となり、
\[1234=10^3× 1+10^2× 2+10^1× 3+10^0× 4\]
と書けます。このことからも10で繰り返し割ることで位の数ごとに分解することができることがわかると思います。
2進数
上でおこなう筆算を2進数でもやってみます。割る数は2進数なので$2$です。
余りを下から並べると$(10011010010)_2$となり、これが$(1234)_{10}$を2進数変換した数となります。
10進数のときのように2の累乗を使った式をつくると、
\begin{align*}1234&=2^{10}× 1+2^9× 0+2^8× 1+2^7× 1\\ &\quad+2^6× 1+2^5× 0+2^4× 1+2^3× 0\\ &\qquad+2^2× 0+2^1× 1+2^0× 0\\ &=2^{10}× 1+2^7× 1+2^6× 1+2^4× 1+2^1× 1\end{align*}
となるため2進数の数の一番下の桁から一の位、二($2^1$)の位、四($2^2$)の位、八($2^3$)の位……となっていることがわかります。
Share:
2021年9月11日
2次関数の頂点と1次関数との交点でできる三角形の面積
「2次関数$y=x^2-4x+1$と1次関数$y=-x+5$の交点2点をx座標の小さい方から$\text{A, B}$とし、2次関数の頂点を$\text{P}$とする。このとき、$△\text{ABP}$の面積を求めよ。」
このような問題はどのように解けばよいでしょうか？
Share:
2021年9月10日
順列はなぜ階乗の分数になるのか？
順列の式は以下のようになります。
\begin{align*}_nP_k&=\frac{n!}{(n-k)!}\tag1\\
&\qquad(n:自然数,k:0\leqq k\leqq nの整数)\end{align*}
なぜ、順列は階乗の分数で表せるのでしょうか？
Share:
2021年9月8日
2021年9月7日
三角形の内角で見る合同条件・相似条件
三角形の合同、あるいは相似を調べるには、角と辺の関係に着目します。
この記事では、特に三角形の角に着目して、合同条件・相似条件にはどのようなものがあるかを見ていきます。
Share:
2021年9月5日
なぜsinを使って三角形の面積が求められるのか？
|
| 図1 三角形\text{ABC} |
\begin{equation}△\text{ABC}=\frac{1}{2}\text{AB}\cdot\text{AC}\sinθ\end{equation}
で求めることができます。
なぜこの式で三角形の面積を求めることができるのでしょうか？
Share:
.png)
2021年9月4日
直交する直線に接する2つの円とその半径
|
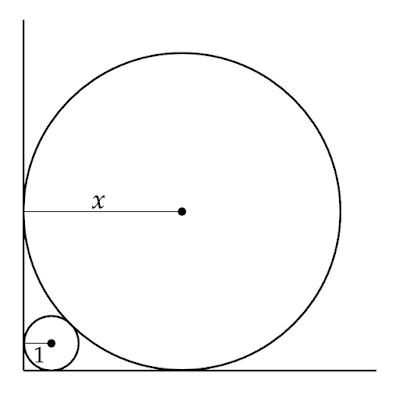
| 図1 直交する直線と2つの円 |
「直交する2本の直線を接線とする円が２つあり、円どうしは交わらず接している。小さい方の円の半径が1であるとき、大きい方の円の半径$x$を求めよ。」
このような問題はどのように解けばよいのでしょうか？
Share:
2021年9月3日
半径が同じ円が2個入った正方形の1辺の長さは？
このような問題はどのように解けばよいのでしょうか？
Share:
2021年9月2日
1つの辺の長さがわかれば面積が求められる特殊な三角形
通常、三角形の面積は
\[(底辺)\times(高さ)\div2\]
で表されるように、底辺と高さという2つの長さがわからないと求められません。
しかし、三角形の中には1辺の長さが分かれば面積が求められるものが存在します。
それはどんな三角形なのか3つの例を見ていきます。
Share:
