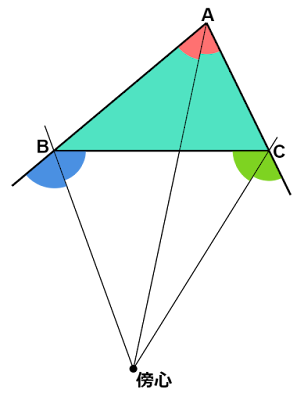
三角形の傍心とは、三角形の1つの内角の二等分線と他の2つの内角に対する外角の二等分線の交点のことで、どの三角形にも傍心が3個存在します。
三角形の1つの内角の二等分線と他の2つの外角の二等分線が1点で交わることを確かめます。
三角形の1つの内角の二等分線と他の2つの外角の二等分線が1点で交わることを確かめます。
$△\text{ABC}$の2つの外角$\text{B, C}$の二等分線の交点を$\text{P}$とします。
点$\text{P}$が傍心であるならば直線$\text{AP}$は内角$\text{A}$の二等分線となるはずなので、これを確かめます。
点$\text{P}$が傍心であるならば直線$\text{AP}$は内角$\text{A}$の二等分線となるはずなので、これを確かめます。
点$\text{P}$から直線$\text{AB, BC, CA}$へそれぞれ垂線をおろし、その足を$\text{Q, R, S}$とします。
すると、外角$\text{B}$の二等分線において2直線がつくる角の二等分線の性質より$\text{PQ}=\text{PR}$、
同様に外角$\text{C}$の二等分線において$\text{PR}=\text{PS}$となるので、$\text{PQ}=\text{PS}$であることがわかります。
$△\text{APQ}$と$△\text{APS}$に着目すると
- 線分$\text{PQ, PS}$はそれぞれ直線$\text{AB, CA}$に対する垂線なので$∠\text{AQP}=∠\text{ASP}=90°$
- また、$\text{PQ}=\text{PS}$
- 共通の辺なので$\text{AP}=\text{AP}$
ゆえに$∠\text{PAQ}=∠\text{PAS}$で、$∠\text{QAS}=∠\text{PAQ}+∠\text{PAS}$より$∠\text{PAQ}=∠\text{PAS}=\dfrac{∠\text{QAS}}{2}$です。
$∠QAS$は2直線$\text{AB, CA}$がつくる角なので直線$\text{AP}$はその二等分線であることがわかります。
以上より、$△\text{ABC}$の内角$\text{A}$の二等分線と外角$\text{B, C}$それぞれの二等分線は1点で交わることを確かめることができました。
これは内角$\text{B}$と外角$\text{A, C}$、内角$C$と外角$\text{A, B}$の場合でも同様なので、傍心は1個の三角形に3個存在することがわかります。
ここで、上述より内角$\text{A}$に対する傍心から直線$\text{AB, BC, CA}$へそれぞれおろした垂線の長さが等しいことがわかりましたが、これは内角$\text{A}$に対する傍心が3直線$\text{AB, BC, CA}$を接線とする円の中心であるということです。この円を傍接円といいます。
同様に内角$\text{B, C}$それぞれに対する傍心も3直線$\text{AB, BC, CA}$を接線とする円の中心となります。
同様に内角$\text{B, C}$それぞれに対する傍心も3直線$\text{AB, BC, CA}$を接線とする円の中心となります。
さらに$△\text{ABC}$の内接円の中心である内心$\text{I}$も3直線$\text{AB, BC, CA}$を接線とする円の中心であるといえるので、1点で交わらない互いに平行でない3直線を接線とする円の中心は3直線によってできる三角形の内心と傍心となります。
Share:
.png)
.png)



