三角関数の加法定理とは、任意の角$α,β$について
\begin{align}\sin(\alpha+\beta)&=\sin\alpha\cos\beta+\cos\alpha\sin\beta\\[1em]\sin(\alpha-\beta)&=\sin\alpha\cos\beta-\cos\alpha\sin\beta\\[1em]\cos(\alpha+\beta)&=\cos\alpha\cos\beta-\sin\alpha\sin\beta\\[1em]\cos(\alpha-\beta)&=\cos\alpha\cos\beta+\sin\alpha\sin\beta\\[1em]\tan(\alpha+\beta)&=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\\[1em]\tan(\alpha-\beta)&=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\end{align}
が成り立つという定理です。
これらはなぜ成り立つのでしょうか?
$\cos$の加法定理
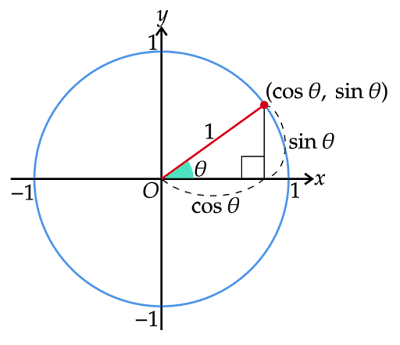
単位円による三角関数の定義は、原点を中心とする半径$1$の円(単位円)においてx軸の正の部分(始線)と反時計回りに$θ$の角をなす半径の円周上の端点の座標を$(\cosθ,\sinθ)$とする、というものでした。この定義をもとに加法定理を導き出します。
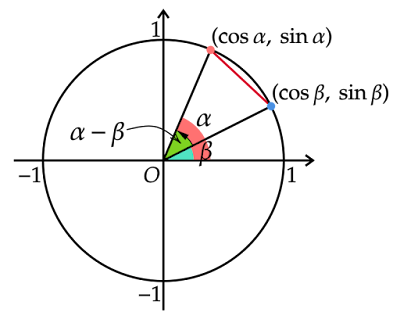
始線とそれぞれ$α,β$の角をなす単位円の半径を考えると、この2本の半径の間の角は$α-β$で表すことができます。$α-β$というのは、$α,β$が始線を基準として測った角であるように、始線と$β$の角をなす半径を基準として測った角となります。
それぞれの半径の円周上の端点の座標は$(\cosα,\sinα),(\cosβ,\sinβ)$なので、この2点間の距離の2乗は
\begin{align*}&(\cos\alpha-\cos\beta)^2+(\sin\alpha-\sin\beta)^2\\[0.5em]=&\cos^2\alpha-2\cos\alpha\cos\beta+\cos^2\beta\\
&\quad+\sin^2\alpha-2\sin\alpha\sin\beta+\sin^2\beta\\[0.5em]=&(\cos^2\alpha+\sin^2\alpha)+(\cos^2\beta+\sin^2\beta)\\
&\quad-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)\\[0.5em]=&1+1-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)&(\because\sin^2\theta+\cos^2\theta=1)\\[0.5em]=&2-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)\tag{a}\end{align*}
となります。これは任意の$α,β$で成り立ちます。
この点と始線と単位円の交点$(1,0)$の距離の2乗を考えると
\begin{align*}&\bigl\{1-\cos(\alpha-\beta)\bigr\}^2+\bigl\{0-\sin(\alpha-\beta)\bigr\}^2\\[0.5em]=&1-2\cos(\alpha-\beta)\\ &\quad+\cos^2(\alpha-\beta)+\sin^2(\alpha-\beta)\\[0.5em]=&1-2\cos(\alpha-\beta)+1&(\because\sin^2\theta+\cos^2\theta=1)\\[0.5em]=&2-2\cos(\alpha-\beta)\tag{b}\end{align*}
となります。
単位円の等しい中心角に対する弦の長さは等しい、ゆえに弦の長さの2乗も等しいので$\text{(a)}=\text{(b)}$より
\begin{align*}2-2\cos(\alpha-\beta)&=2-2(\cos\alpha\cos\beta+\sin\alpha\sin\beta)\\[0.5em]\cos(\alpha-\beta)&=\cos\alpha\cos\beta+\sin\alpha\sin\beta\end{align*}
となり、$(4)$が得られます。
$(4)$の$β$を$-β$に置き換えると
\begin{align*}\cos\bigl\{\alpha-(-\beta)\bigr\}&=\cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta)\\[0.5em]\cos(\alpha+\beta)&=\cos\alpha\cos(-\beta)+\sin\alpha\sin(-\beta)\end{align*}
三角関数の性質$\sin(-θ)=-\sinθ,\cos(-θ)=\cosθ$より
\begin{align*}\cos(\alpha+\beta)&=\cos\alpha\cos\beta+\sin\alpha(-\sin\beta)\\[0.5em]&=\cos\alpha\cos\beta-\sin\alpha\sin\beta\end{align*}
となり、$(3)$を得ます。
$\sin$の加法定理
$\sin(α+β)$は三角関数の性質$\sinθ=\cos(90°-θ)$より
\begin{align*}\sin(\alpha+\beta)&=\cos\bigl\{90°-(\alpha+\beta)\bigr\}\\[0.5em]&=\cos(90°-\alpha-\beta)\\[0.5em]&=\cos\bigl\{(90°-\alpha)-\beta\bigr\}\end{align*}
と表せます。これは$(4)$の左辺の$α$を$90°-α$に置き換えたものです。
したがって、
\begin{align*}\cos\bigl\{(90°-\alpha)-\beta\bigr\}&=\cos(90°-\alpha)\cos\beta+\sin(90°-\alpha)\sin\beta\\[0.5em]\sin(\alpha+\beta)&=\cos(90°-\alpha)\cos\beta+\sin(90°-\alpha)\sin\beta\end{align*}
が成り立ちます。
これは、三角関数の性質$\sin(90°-θ)=\cosθ,$$\cos(90°-θ)=\sinθ$より
\[\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\]
と書け、$(1)$を得ます。
同様に$\sin(α-β)$は三角関数の性質$\sinθ=\cos(90°-θ)$より
\begin{align*}\sin(\alpha-\beta)&=\cos\bigl\{90°-(\alpha-\beta)\bigr\}\\[0.5em]&=\cos(90°-\alpha+\beta)\\[0.5em]&=\cos\bigl\{(90°-\alpha)+\beta\bigr\}\end{align*}
と表せます。これは$(3)$の左辺の$α$を$90°-α$に置き換えたものです。
したがって、
\begin{align*}\cos\bigl\{(90°-\alpha)+\beta\bigr\}&=\cos(90°-\alpha)\cos\beta-\sin(90°-\alpha)\sin\beta\\[0.5em]\sin(\alpha-\beta)&=\cos(90°-\alpha)\cos\beta-\sin(90°-\alpha)\sin\beta\end{align*}
が成り立ちます。
これは、三角関数の性質$\sin(90°-θ)=\cosθ,$$\cos(90°-θ)=\sinθ$より
\[\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta\]
と書け、$(2)$を得ます。
$\tan$の加法定理
$(5),(6)$は$(1)~(4)$を利用して導きます。
$\tan(α+β)$は三角関数の相互関係$\tanθ=\dfrac{\sinθ}{\cosθ}$より
\[\tan(\alpha+\beta)=\frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}\]
と表せます。
$(1),(3)$より
\[\tan(\alpha+\beta)=\frac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta}\]
分母と分子を$\cosα\cosβ$で割ると
\begin{align*}\tan(\alpha+\beta)&=\frac{\cfrac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{\cfrac{\cos\alpha\cos\beta-\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}\\[0.5em]&=\frac{\cfrac{\sin\alpha\cos\beta}{\cos\alpha\cos\beta}+\cfrac{\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{\cfrac{\cos\alpha\cos\beta}{\cos\alpha\cos\beta}-\cfrac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}\\[0.5em]&=\frac{\cfrac{\sin\alpha}{\cos\alpha}+\cfrac{\sin\beta}{\cos\beta}}{1-\cfrac{\sin\alpha}{\cos\alpha}\cdot\cfrac{\sin\beta}{\cos\beta}}\\[0.5em]&=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\end{align*}
となり、$(5)$を得ます。
同様に$\tan(α-β)$は三角関数の相互関係$\tanθ=\dfrac{\sinθ}{\cosθ}$より
\[\tan(\alpha-\beta)=\frac{\sin(\alpha-\beta)}{\cos(\alpha-\beta)}\]
と表せます。
$(2),(4)$より
\[\tan(\alpha-\beta)=\frac{\sin\alpha\cos\beta-\cos\alpha\sin\beta}{\cos\alpha\cos\beta+\sin\alpha\sin\beta}\]
分母と分子を$\cosα\cosβ$で割ると
\begin{align*}\tan(\alpha-\beta)&=\frac{\cfrac{\sin\alpha\cos\beta-\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{\cfrac{\cos\alpha\cos\beta+\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}\\[0.5em]&=\frac{\cfrac{\sin\alpha\cos\beta}{\cos\alpha\cos\beta}-\cfrac{\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{\cfrac{\cos\alpha\cos\beta}{\cos\alpha\cos\beta}+\cfrac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}\\[0.5em]&=\frac{\cfrac{\sin\alpha}{\cos\alpha}-\cfrac{\sin\beta}{\cos\beta}}{1+\cfrac{\sin\alpha}{\cos\alpha}\cdot\cfrac{\sin\beta}{\cos\beta}}\\[0.5em]&=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\end{align*}
となり、$(5)$を得ます。
Share:
.png)



