座標平面上の点$\text{A}$をある点を中心に反時計回りに$φ$だけ回転移動させたとき、移動後の点の座標はどのように表せるでしょうか？
点$\text{A}$の直交座標を$(a,
b)$、回転移動後の点を$\text{A'}$、その座標を$(a', b')$とおきます。
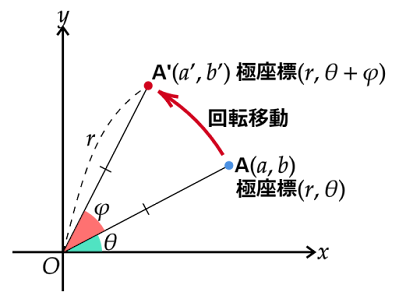
原点を中心に回転移動
極座標を利用して考えます。
\begin{align}a&=r\cos\theta\\[0.5em]b&=r\sin\theta\end{align}
という関係が成り立ちます。
原点を中心に反時計回りに$φ$だけ回転移動した後の点$\text{A'}$の極座標は$(r,
θ+φ)$となり、これを直交座標に変換すると$(a', b')=\bigl(r\cos(θ+φ),
r\sin(θ+φ)\bigr)$となります。
ここで、三角関数の加法定理より
これが点$\text{A}(a, b)$を原点を中心に反時計回りに$φ$だけ回転移動させた後の点の直交座標を求める式となります。
\begin{align*}a'&=r\cos(\theta+\varphi)\\[0.5em]&=r(\cos\theta\cos\varphi-\sin\theta\sin\varphi)\\[0.5em]&=r\cos\theta\cdot\cos\varphi-r\sin\theta\cdot\sin\varphi\\[1em]b'&=r\sin(\theta+\varphi)\\[0.5em]&=r(\sin\theta\cos\varphi+\cos\theta\sin\varphi)\\[0.5em]&=r\sin\theta\cdot\cos\varphi
+r\cos\theta\cdot\sin\varphi\end{align*}
となり、$(1), (2)$を代入すると
\begin{align*}\large
a'&\large=a\cos\varphi-b\sin\varphi\\[1em]\large
b'&\normalsize=b\cos\varphi
+a\sin\varphi\\[0.5em]&\large=a\sin\varphi +b\cos\varphi\end{align*}
となります。これが点$\text{A}(a, b)$を原点を中心に反時計回りに$φ$だけ回転移動させた後の点の直交座標を求める式となります。
直交座標を列ベクトルで表したとき、上記のような式を得る行列の積は
\[\begin{pmatrix}a'\\
b'\end{pmatrix}=\begin{pmatrix}\cos\varphi&-\sin\varphi\\
\sin\varphi&\cos\varphi\end{pmatrix}\begin{pmatrix}a\\
b\end{pmatrix}\]
であり、このときの行列$\begin{pmatrix}\cos\varphi&-\sin\varphi\\
\sin\varphi&\cos\varphi\end{pmatrix}$を回転行列といいます。
点$\text{P}(p, q)$を中心に回転移動
点$\text{A}$を点$\text{P}(p,
q)$を中心に反時計回りに$φ$だけ回転移動させた後の座標は、平行移動と上述の原点を中心に回転移動の2つを利用して求めます。
.png)
平行移動後の点を$\text{B}$とすると、点$\text{B}$の座標は$(a-p, b-q)$となります。
点$\text{B}$を原点$\text{O}$を中心に反時計回りに$φ$だけ回転移動させた後の点$\text{B'}$の座標は上記より$\bigl((a-p)\cosφ-(b-q)\sinφ,
(a-p)\sinφ+(b-q)\cosφ\bigr)$となります。
.png)
したがって、点$\text{B'}$を原点$\text{O}$から点$\text{P}$まで平行移動するときと同じ移動量で平行移動させると平行移動後の点は対応する点$\text{A'}$となり、その座標は$\bigl((a-p)\cosφ-(b-q)\sinφ+p, (a-p)\sinφ+(b-q)\cosφ+q\bigr)$となります。
すなわち、
\begin{align*}\large a'&\large=(a-p)\cos\varphi-(b-q)\sin\varphi
+p\\[1em]\large b'&\large=(a-p)\sin\varphi-(b-q)\cos\varphi
+q\end{align*}
が点$\text{A}(a, b)$を点$(p,
q)$を中心に反時計回りに$φ$だけ回転移動させた後の座標を求める式となります。
Share:
