正三角形の中線は垂直二等分線かつ角の二等分線になる？

　正三角形の中線は垂直二等分線や角の二等分線になることができるのでしょうか？

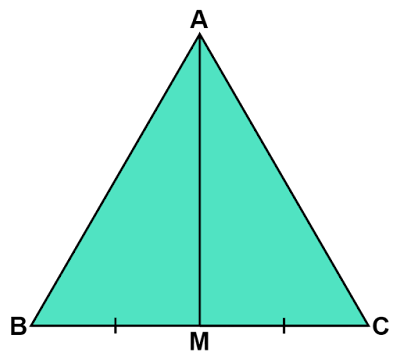
　正三角形$\text{ABC}$の頂点$\text{A}$と辺$\text{BC}$の中点$\text{M}$を結ぶ中線$\text{AM}$を引き、$△\text{ABM}$と$△\text{ACM}$をつくります。

この2つの三角形は

• 正三角形$\text{ABC}$より、$\text{AB}=\text{AC}$
• 点$\text{M}$は$\text{BC}$の中点なので$\text{BM}=\text{CM}$
• $\text{AM}$は共通の辺なので$\text{AM}=\text{AM}$

であることから、3組の辺がそれぞれ等しいので$△\text{ABM}$と$△\text{ACM}$は合同であることがわかります。

　このことから$∠\text{BAM}=∠\text{CAM}$であるから中線$\text{AM}$は$∠\text{A}$の二等分線であることがわかります。
また、$∠\text{AMB}=∠\text{AMC}$、$∠\text{BMC}=180°$であることから$∠\text{AMB}=∠\text{AMC}=90°$
このことと$\text{BM}=\text{CM}$であることから中線$\text{AM}$は$\text{BC}$の垂直二等分線であることがわかります。

以上は二等辺三角形の頂点からのびる中線についても同様に言えます。

さらに、$\text{AB}=\text{BC}=\text{CA}$であることから$\text{AB, CA}$の中線を$\text{N, O}$とし、上記と同様にして中線$\text{CN}$が$\text{AB}$の垂直二等分線かつ$∠\text{C}$の二等分線、中線$\text{BO}$が$\text{CA}$の垂直二等分線かつ$∠\text{B}$の二等分線であることを示すことができます。

したがって、正三角形の中線は交わる辺の垂直二等分線であり、通る頂点における内角の二等分線であることがわかります。

関連：二等辺三角形の特徴

関連：頂角が$60°$の二等辺三角形が正三角形であることの証明