2022年12月31日
2022年12月25日
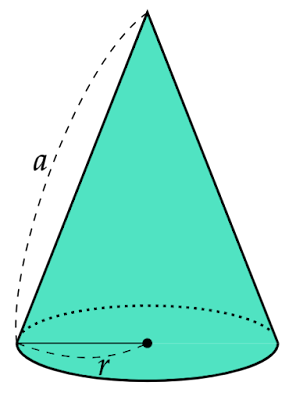
円錐の底面の半径と母線の長さの比
2022年12月23日
この多項式は3の倍数になる?
2022年12月21日
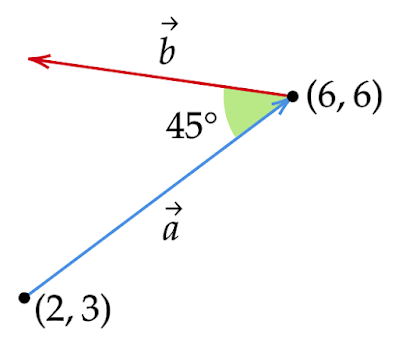
x切片とy切片だけがわかっているときの直線の式
2022年12月18日
0乗はなぜ1になる?
2022年12月17日
二重、三重になっている根号はどうやって1つにする?
上のように根号で入れ子になっている数は1つの根号だけを使って表すことができます。
どのように考えれば1つの根号で表すことができるのでしょうか?
2022年12月15日
分数式を部分分数分解する(2)
(1)$\large\dfrac{4x-9}{2x^2-x-15}$
(2)$\large-\dfrac{4x}{(x+3)^2(3x+9)}$
(3)$\large\dfrac{x^3-4x^2-3x+2}{x^2+4x-5}$」このような問題はどのように解けばよいのでしょうか?
2022年12月12日
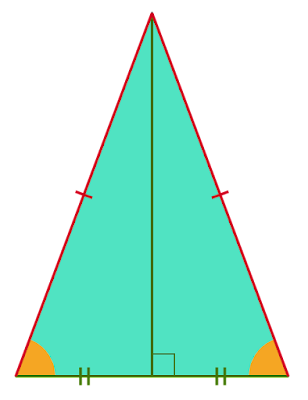
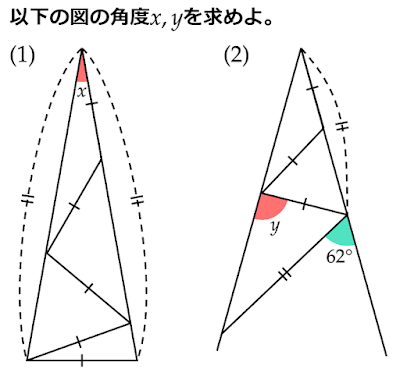
二等辺三角形の特徴
1.の特徴は名称通り、定義通りのものですが、なぜ2.、3.の特徴を持つ三角形も二等辺三角形であると言えるのでしょうか?
2022年12月10日
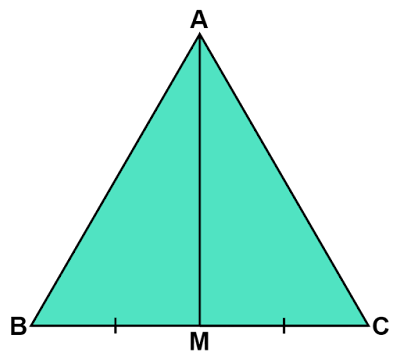
正三角形の中線は垂直二等分線かつ角の二等分線になる?
2022年12月9日
分数式を部分分数分解する
(1)$\large\dfrac{3}{(x+2)(x-5)}$
(2)$\large\dfrac{2x^2-3x+7}{(x+1)^3}$
(3)$\large\dfrac{x+4}{x(x-2)^2}$」このような問題はどのように解けばよいのでしょうか?
2022年12月6日
直角三角形の合同条件・相似条件
- 内角の1つが必ず$90°$である。
- 3辺の長さは必ず三平方の定理$a^2+b^2=c^2$を満たす。
2022年12月4日
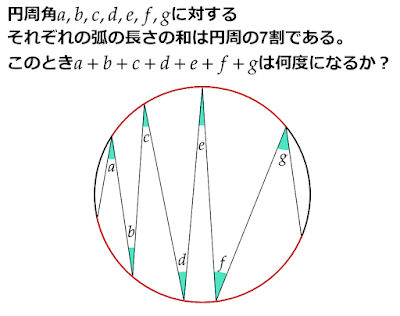
交わる2直線間を等しい長さの線分で分割したときの角度
2022年12月2日
3つの外接する円の共通接線の交点と三角形の関係は?
円$\text{O$_1$}$と$\text{O$_2$}$の接点$\text{Q}$を通る共通接線、円$\text{O$_2$}$と$\text{O$_3$}$の接点$\text{R}$を通る共通接線、円$\text{O$_3$}$と$\text{O$_1$}$の接点$\text{S}$を通る共通接線は点$\text{P}$で交わる。
このとき以下の問いに答えよ。
(1)各円の中心を頂点とする$△\text{O$_1$O$_2$O$_3$}$において点$\text{P}$はなんという点であるか?三角形に関係する点の名称で答えよ。
(2)$\text{PQ}$の長さを求めよ。」2022年11月29日
2022年11月26日
2022年11月24日
積和の公式・和積の公式
2022年11月23日
余弦定理 なぜ成り立つ?
2022年11月21日
正弦定理 なぜ成り立つ?
なぜこのような式になるのでしょうか?
2022年11月20日
三角形の1辺の長さと両端の角から外接円の半径を求める
2022年11月17日
x^2の係数が1でない2次式を工夫して因数分解する
これを工夫して少し簡単に因数分解してみます。
2022年11月15日
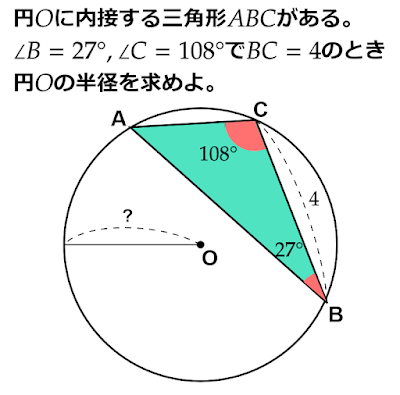
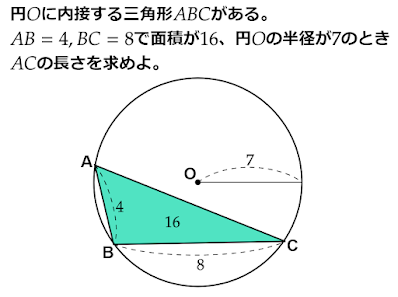
円に内接する三角形の1辺の長さは?(三角形の3辺と面積、外接円の半径の関係)
この三角形の2辺が$\text{AB}=4,\text{BC}=8$で面積が$16$、円$\text{O}$の半径が$7$のとき$\text{AC}$を求めよ。」
このような問題はどのように解けばよいのでしょうか?
2022年11月13日
2次不等式のように解く不等式
(1)$\large -2\sin^2\theta-5\sin\theta+3>0\quad(0\leqq\theta<2\pi)$
(2)$\large 2^{2x}-2^{x+1}-8\leqq0$
(3)$\large x+2\sqrt{x}-15>0$」2022年11月12日
log0はどんな数?
$\log{0}$はどのような数になるでしょうか?
2022年11月9日
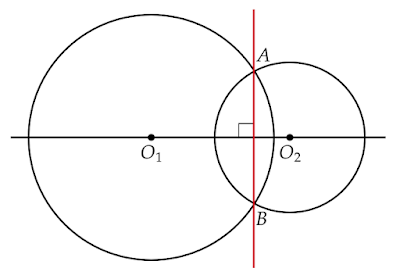
2円の異なる2つの交点を通る直線と2つの中心を通る直線の関係
2022年11月6日
半径と同じ長さの弦に対する円周角は何度?
2022年11月5日
実数の符号を反対にするには何乗すれば良い?
2022年11月3日
虚数乗して実数になる数は?
2022年11月1日
合同式とは? 余りに着目した関係式
どういう性質があるのでしょうか?
2022年10月29日
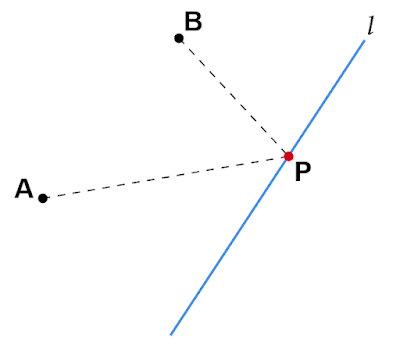
直線上の点を経由したときの2点の最短距離は?
2022年10月28日
高さが等しいルーローの多角形と円の周の長さ
ルーローの多角形の周の長さと同じ高さを持つ円の周の長さにはどのような関係があるでしょうか?
2022年10月25日
2次不等式を解く(2)
「次の2次不等式を解け。
(1)$\large x^2-3x-18<0$
(2)$\large x^2+6x+8\geqq0$
(3)$\large -x^2+2x-3<0$
(4)$\large x^2-4x+5\leqq0$」
2022年10月22日
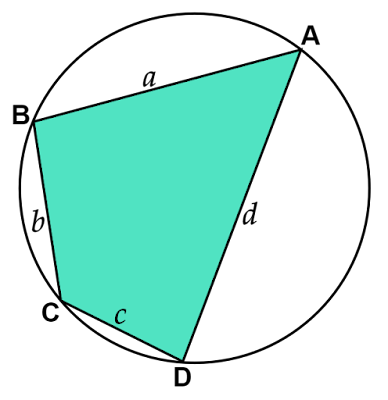
円に内接する四角形の面積を求める方法 ブラーマグプタの公式
なぜこの式で面積を求めることができるのでしょうか?
2022年10月21日
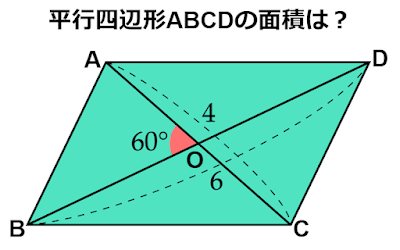
対角線の長さとなす角から平行四辺形の面積を求める
このような問題はどのように解けばよいのでしょうか?
2022年10月20日
三角形の面積を求める式いろいろ
2022年10月16日
ヘロンの公式 三角形の3辺から面積を求める公式
なぜ、この公式で面積を求められるのでしょうか?
2022年10月14日
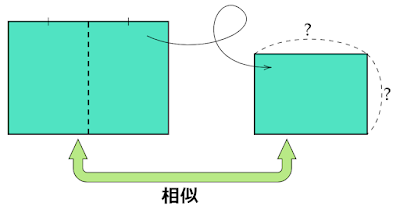
半分に分割しても相似な長方形の縦横比は?
2022年10月12日
ルーローの三角形の周の長さと面積を求める
この図形を作図するときにもとになった正三角形の1辺の長さが$2$であったとき、この図形の周の長さと面積を求めよ。」
このような問題はどのように解けばよいのでしょうか?
2022年10月8日
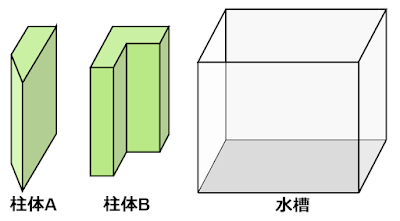
柱体の底面の面積比は? 水の体積から求める
(1)水槽と柱体$A$の底面の面積比を求めよ。
(2)柱体$A$と柱体$B$の底面の面積比を求めよ。」
2022年10月5日
x^2の係数が1以外の2次式の因数分解はどうやる?
$x^2$の係数が1以外の2次式、つまり$px^2+qx+r$の因数分解をするにはどうすればよいのでしょうか?
2022年10月2日
x^2の係数が1の2次式の因数分解はどうやる?
$x^2$の係数が$1$の2次式、つまり$x^2+px+q$の因数分解をするにはどうすればよいのでしょうか?
2022年10月1日
勾配伸び率とは? 3°刻みで勾配伸び率を求めてみる
その意味と3°刻みでの各角度における勾配伸び率がどうなるのかを調べてみました。
2022年9月29日
勾配率とは? 3°刻みで勾配率を求めてみる
その意味と3°刻みでの各角度における勾配率はどうなるのかを調べてみます。
2022年9月28日
ホテルの客室番号は? 欠番のある客室番号の計算
(1)小さい順で45番目の客室番号は何番か?
(2)小さい順で300番目の客室番号は何番か?
(3)”$258$”号室の客室は小さい順で何番目か?」
2022年9月25日
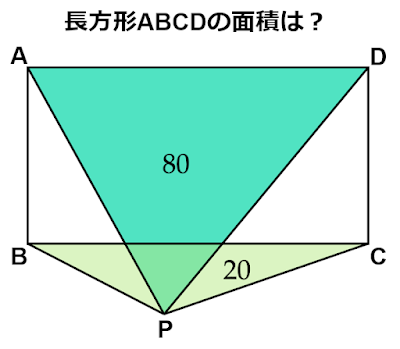
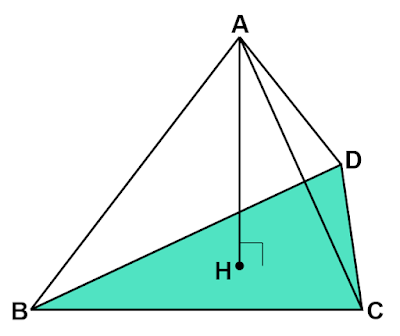
三角形の面積から長方形の面積を求める
$△\text{PAD}$の面積が$80$、$△\text{PBC}$の面積が$20$のとき、長方形$\text{ABCD}$の面積を求めよ。」
このような問題はどのように解けばよいでしょうか?
2022年9月24日
1つの紙を余すことなく切り分けるには?
(1)正方形
(2)短辺と長辺の長さの比が$1:2$の長方形
(3)短辺と長辺の長さの比が$2:3$の長方形」
2022年9月23日
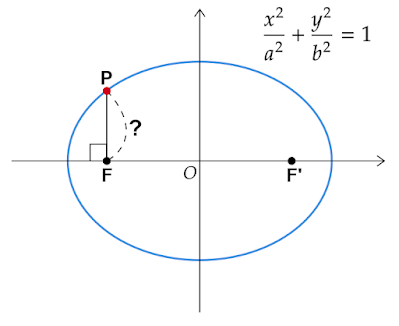
楕円の焦点から引いた垂線の長さは?
2022年9月20日
3つの積から3つの数を求める
「3つの異なる整数$A,B,C$がある。$A$と$B$を掛けると$-57$、$B$と$C$を掛けると$21$、$C$と$A$を掛けると$-133$となる。$A,B,C$を求めよ。」
2次方程式が2解を持つときに重解が含まれるのはなぜ?
2022年9月17日
楕円の2つの焦点からの和と長軸の長さが等しくなるのはなぜなのか?
これはなぜなのでしょうか?
2022年9月15日
楕円の長軸と短軸の各部分の長さは?
この長軸と短軸そのものの長さや、焦点で区切られた線分の長さはどうなっているのでしょうか?
2022年9月13日
主軸がx軸でもy軸でもない楕円の方程式はどうなる?
2022年9月11日
単位ベクトルとは?
もう1つのベクトルに垂直なベクトル成分は?
(1)$\large\vec{a}=(-5,-7),\vec{b}=(-1,2)$
(2)$\large\vec{a}=(4,-1),\vec{b}=(3,4)$」
2022年9月10日
放物線の接線の方程式
なぜ、このような式で表されるのでしょうか?
2022年9月9日
双曲線の接線の方程式
なぜ、このような式で表されるのでしょうか?
楕円の接線の方程式
なぜ、このような式になるのでしょうか?
2022年9月7日
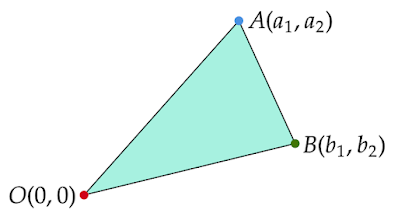
原点と他の2点からつくられる三角形の面積を求める
2022年9月5日
この点は領域に入る?入らない?
(1)$\large y<3x+2\quad[(-1,3)]$
(2)$\large y>-x^2+3x+4\quad[(3,5)]$
(3)$\large \dfrac{x^2}{3}+\dfrac{y^2}{4}\leqq2\quad[(1,-2)]$」
2022年9月4日
不等式と領域 どの部分?
(1)$\large y\geqq -2x+3$
(2)$\large y<x^2+4x+1$
(3)$\large x^2+y^2<4$」
2022年9月3日
解から2次方程式を求める
(1)$\large x=0,3$
(2)$\large x=\pm5$
(3)$\large x=2$
(4)$\large x=2-\sqrt{3},2+\sqrt{3}$
(5)$\large x=1+\sqrt{3},3-\sqrt{3}$」
2022年9月1日
1次不定方程式の整数解を求める(1)
(1)$\large 2x-y=3$
(2)$\large 3x+4y=2$」このような問題はどのように解けばよいでしょうか?
2022年8月28日
二重の絶対値を含む方程式
(1)$\large\left||x-3|-2\right|=2$
(2)$\large\left||5-2x|+3\right|=-1$
(3)$\large\left||x^2-2x-3|-5\right|=0$
(4)$\large\left||x^2+3x-18|+x-3\right|=0$」このような問題はどのように解けばよいでしょうか?
2022年8月25日
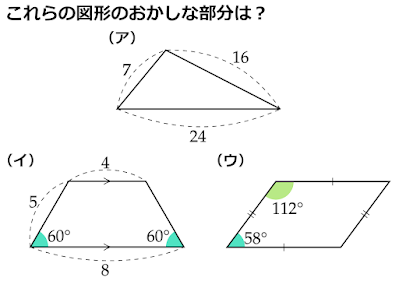
ありえない図形 なぜ?
2022年8月21日
互いに素とは?
ユークリッドの互除法 最大公約数を求める方法
ユークリッドの互除法とは、2つの整数の最大公約数を見つけるための方法で、以下の手順で見つけます。
- $A$と$B$の大きい方を小さい方で割り、余り$r_1$を求めます。
- $A$か$B$の割る数になった方を$r_1$で割り、余り$r_2$を求めます。
2022年8月20日
旅人算の問題 追いつくまでにかかる時間と距離は?
(1)BさんがAさんに追いつくのはBさんが歩きだしてから何分後か?
(2)追いつくまでにAさんとBさんは歩きだした地点に何回戻ってくるか?」
2022年8月19日
定積分の1/6公式
なぜ、これが成り立つのでしょうか?2通りの方法で確かめてみます。
2022年8月17日
通過算の問題 トンネルと列車の長さは?
「長さ$62$mの列車Aは秒速$24$mで走りトンネルを通過しきるのに$13$秒かかる。列車Bは同じトンネルを通過しきるのに$9$秒かかる。このとき列車Aと列車Bの速度の比は$3:4$であった。
トンネルと列車Bの長さはそれぞれ何mかを求めよ。」
2022年8月15日
摂氏温度と華氏温度の変換
華氏温度は【セ氏】(中略)一気圧における水の氷点を零度、沸点を一〇〇度として、その間を一〇〇等分したもの。
【華氏】(中略)一気圧における水の凝固点を三二度、沸点を二一二度として、その間を一八〇等分したもの。
このことから、摂氏温度を華氏温度に変換、また華氏温度を摂氏温度に変換するにはどのような計算をおこなえばよいのでしょうか?
2022年8月13日
2次方程式の2解が○○である条件(2)
「2次方程式$x^2+3kx-2k=0$の2解が$-2\leqq x<\dfrac{1}{2}$の範囲にあるときの$k$を求めよ。」
2次方程式の2解が○○である条件
(1)2解ともに正
(2)2解ともに$-1$以下
(3)2解の符号が異なる」
2022年8月10日
2次方程式が2解を持つ条件
(1)異なる2解を持つ
(2)2解を持つ
(3)2解ともに正」
2022年8月8日
2次方程式の解の公式と判別式
なぜ、このような式になるのでしょうか?
また、判別式$D=b^2-4ac$とはどのような関係があるのでしょうか?
2022年8月7日
2022年8月6日
1辺の長さが1の正五角形の幅と高さは?
2022年8月5日
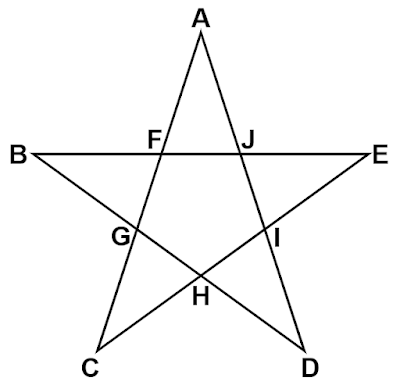
五芒星の各線分の長さ
2022年8月2日
整数Nの整数倍の余り、2乗の余り
(1)$3N$
(2)$N^2$
(3)$N^2+3N+1$」
2022年7月31日
元金均等返済方式の返済額の計算式
2022年7月29日
元利均等返済方式の返済額の計算式
元利均等返済方式とは、常に一定額を返済していく方式のことです。
返済額の計算方法は年々返済する場合
\begin{align*}P_b&=\frac{P_rA(1+A)^n}{(1+A)^n-1}\\ &(P_b:返済額,P_r:借入元金,A:年率,n:返済期間)\end{align*}
となります。
共役複素数の性質
複素数$z=a+bi,w=c+di$ $(a,b,c,d:実数)$について、それぞれの共役複素数は$\bar{z}=a-bi,\bar{w}=c-di$となります。
これらをもちいて共役複素数の性質とそれらが成り立つことを見ていきます。
2022年7月27日
合成ベクトルの内積
2022年7月26日
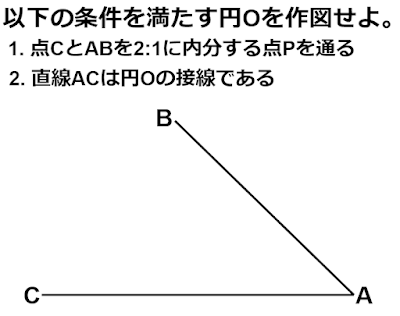
2点を通る円の作図
条件1:円$\text{O}$は点$\text{C}$と線分$\text{AB}$を$2:1$に内分する点$\text{P}$を通る。
条件2:円$\text{O}$は直線$\text{AC}$を接線とする。」
2022年7月24日
絶対値のある2次方程式の実数解の個数(グラフ不使用)
「$|x^2-3x-18|=x+k$が実数解をもつときの$k$の値の範囲を実数解の個数ごとに場合分けをして答えよ。」
絶対値を含む2次不等式を解く
(1)$\large |x^2-5x+6|>3$
(2)$\large |2x^2-5x-3|\leqq x$」
2022年7月23日
絶対値を含む1次不等式を解く(2)
(1)$|x-1|>2x-1$
(2)$|x+1|\leqq-\dfrac{1}{2}x+1$」
2022年7月22日
絶対値を含む1次不等式を解く(1)
(1)$\large |x|<3$
(2)$\large |x|\geqq5$
(3)$\large |x+2|\leqq2$
(4)$\large |x-3|>1$
(5)$\large |x-5|>-2$
(6)$\large |x+1|\leqq-4$」このような問題はどのように解けばよいでしょうか?
2022年7月20日
2次関数の異なる2接線の交点の座標を求める
このような問題はどのように解けばよいでしょうか?
2022年7月18日
三平方の定理 正方形以外の図形
2022年7月17日
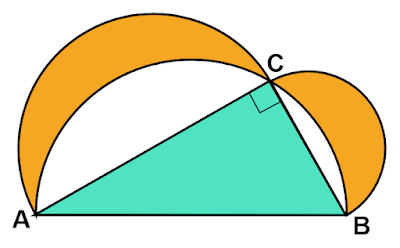
ヒポクラテスの定理
なぜこの関係が成り立つのでしょうか?
2022年7月15日
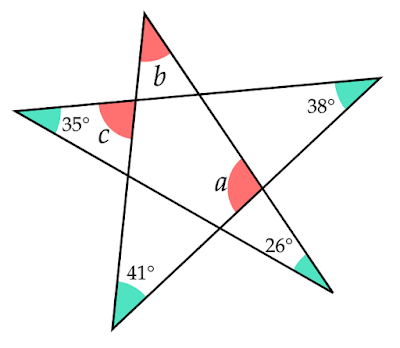
星型五角形の先端の角度の和はなぜ180°なのか?
2022年7月14日
星型五角形の角度を求める
2022年7月13日
対数の計算法則を利用した問題
(1)$\large \log(MN)^p=\log{N^\square}+\log{M^pN^3}$
(2)$\large \log\frac{M}{N}=\log\frac{1}{M}-\log\square$
(3)$\large \log{M^p}=\frac{1}{p}\log{M^\square}$」このような問題はどのように解けばよいでしょうか?
2022年7月12日
なぜ複素数は|a+bi|^2=(a+bi)^2とすることができないのか?
実数$a,b$について
\[|a+b|^2=(a+b)^2\]
という式が成り立ちます。しかし、複素数$a+bi$の場合だと
\[|a+bi|^2=(a+bi)(a-bi)\]
となります。
2022年7月9日
1次方程式をグラフで考える
\[-3x+7=x+5\]
について考えます。
連立方程式をグラフで考える
連立方程式をグラフで考えるとどうなるのでしょうか?
2022年7月8日
連立方程式を解く
2022年7月6日
関数のグラフの対称移動
なぜこのように表すことができるのかをグラフ上の点に着目して考えます。
2022年7月2日
極限値と極値の違いは?
極限値と極値、よく似ている単語ですがどのような違いがあるのでしょうか?
2022年7月1日
2次関数の頂点が最大・最小となる条件
(1)頂点で最大となる。
(2)頂点で最小となる。」
2022年6月29日
最大値・最小値が「ない」ときとは?
最大値や最小値が「ない」ときとはどのようなときなのでしょうか?
2022年6月26日
分数式に代入して整数値を出せる自然数は何個?
このような問題はどのように解けばよいでしょうか?
2022年6月25日
合成関数の最大値・最小値を求める
(1)
このような問題はどのように解けばよいでしょうか?
2022年6月24日
2次関数のグラフの平行移動
2022年6月22日
2直線の交点と他の一点を通る直線の方程式を求める
このような問題はどのように解けばよいでしょうか?
2022年6月20日
「pならばq」を否定すると?
2022年6月19日
三角関数の合成 sinやcosの係数をどうするか?
三角関数の合成とは同じ角度が入っている三角関数の和や差、すなわち$a\sinθ+b\cosθ$や$a\sinθ-b\cosθ$を1つの三角関数で表す方法のことです。
公式1
公式2
これらは加法定理を利用して導くことができます。
2022年6月18日
円周角の定理 なぜ成り立つのか?
この円周角の定理はなぜ成り立つのでしょうか?
2022年6月17日
2次方程式の両辺をxで割って解いてはいけないのはナゼ?
2022年6月14日
極限の不定形(∞-∞、0×∞)はなぜ極限値を出すことができないのか?
\[\Large\lim_{x\to\infty}(x-x^2)\]
この極限はどうなるでしょうか?
このまま極限を計算しようとすると$x\to\infty$のとき$x^2\to\infty$なので、
\[\lim_{x\to\infty}(x-x^2)=\infty-\infty\]
となります。これは一例ですが$\infty-\infty$は不定形と呼ばれるもので、この状態では極限値を求めることはできません。
2022年6月12日
連続する3つの整数の積はなぜ6の倍数なのか?
連続する3つの整数の積はなぜ6の倍数になるのでしょうか?
2022年6月9日
割合と百分率の違いは?
2022年6月8日
ヴィヴィアーニの定理の拡張についての考察
Wikipediaのヴィヴィアーニの定理のページにて正多角形と等角多角形、凸な等辺多角形においても成り立つとの記述があったので、このヴィヴィアーニの定理の拡張を自分なりに考察してみました。
四角形については以前の記事で言及しているので五角形をもちいます。
2022年6月5日
積の微分・商の微分
対数関数を指数に持つ指数関数の微分
(1)$\large e^{\log_e{x}}$ $\large(x>0)$
(2)$\large e^{x\log_e{2}}$
(3)$\large e^{\log_3{x}}$ $\large(x>0)$」
2022年6月4日
指数関数の微分いろいろ
2022年6月2日
小数と分数を含む1次方程式を解く
このような問題はどのように解けばよいでしょうか?
底の異なる指数のついた数同士の積と商
底の異なる指数のついた数同士の積と商はどのような変形ができるでしょうか?
2022年5月30日
指数の計算法則
2022年5月29日
おうぎ形の弧の長さや面積はなぜ角度の分数を使って求められるのか?
なぜこのような計算をするのでしょうか?
2022年5月28日
仕事算の問題を解く
「同じ仕事を終わらせるのにAさんは4日、Bさんは8日、Cさんは10日かかる。
この仕事をAさんとCさんの2人で最初の2日間こなし、翌日残りをBさん1人に引き継いだ。Bさんは何日で仕事を終わらせることができるか?」
何の2乗?何のべき乗?
2022年5月27日
1階線形微分方程式の解の公式
2022年5月24日
2円の交点を通る円・直線の方程式
2022年5月22日
整数は何桁?0でない数が現れるのは小数第何位?
(1)$3^{30}$は何桁の整数か?
(2)$0.3^{15}$は小数第何位に$0$でない数が現れるか?」このような問題はどのように解けばよいのでしょうか?
2022年5月21日
円の接線の方程式の公式
なぜこれが円の接線の方程式となるのでしょうか?
円の方程式を接線の方程式の公式を利用して求める
「直線$l:2x-y=10$を接線とし点$(1,2)$を中心とする円の方程式を求めよ。」
2022年5月19日
絶対値がある2次方程式を解く
このような問題はどのように解けばよいのでしょうか?
絶対値が2つある方程式を解く
「次の方程式を解け。」
このような問題はどのようにして解けばよいでしょうか?
2022年5月17日
f(x)とg(x)を含む恒等式 f(x)とg(x)を求める
ただし、$f(x),g(x)$の係数・定数項はすべて整数である。」
このような問題はどのように求めればよいでしょうか?
2022年5月13日
斜辺と鋭角の1つの角度しかわからない直角三角形の面積を求めるには
2022年5月11日
2022年5月10日
方程式の解が複数あるときのカンマの意味は「または」?「かつ」?どっち?
例えば$x^2+x-2=0$の解を$x=-2,1$のように書きますが、$-2$と$1$の間にある「,(カンマ)」には「または」と「かつ」のどちらの意味があるでしょうか?
2022年5月8日
重複のある文字の並べ方は何通り?
2022年5月7日
不等号が2つある2次不等式を解く
\[\Large -8\leqq x^2+6x\leqq16\]
2022年5月5日
2進数を5進数に変換する
2022年5月4日
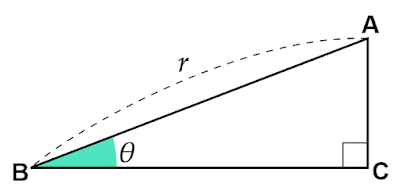
1次関数と三角比
円は何回転する? 円の周りを転がる円
2022年5月3日
sin10°、cos10°、tan10°はどんな数?
10は3の倍数ではないので、これまでに求めた角度における三角比を加法定理を利用して求めることはできません。
なので、3倍角を利用して求めてみます。
2022年4月30日
底の異なる指数方程式を解く(2)
「底の異なる指数方程式を解く(1)」でもちいた2通りの解き方で解いてみます。
2022年4月29日
底の異なる指数方程式を解く(1)
(1)$2^x=5^x$
(2)$2^{x+1}=5^x$」
このような問題はどのように解けばよいでしょうか?
2022年4月28日
csc(x)、sec(x)、cot(x)の微分
2022年4月27日
x^n(xの累乗)の微分
2022年4月26日
tanの微分いろいろ
2022年4月25日
付け足して取り除くという計算テク
2022年4月24日
時速を分速に変換するには
時速を分速に変換するにはどのようにすればよいのでしょうか?
2022年4月23日
正四面体の対辺が互いに垂直であることを確かめる
座標平面における回転行列
文字式を含む分数の約分
文字を含む分数の約分はどのようにすればよいでしょうか?
2022年4月21日
方程式を解く4つの基本操作
方程式を解くために使用する基本的な方法にはどのようなものがあるでしょうか?
2022年4月20日
正四面体の頂点から対面におろした垂線はどこで交わる?
(e^x)'=e^xであることを確かめるためには
2022年4月19日
2次方程式のように解く方程式
2次方程式ではないですが2次方程式の解き方で解を求めることができる方程式の例を4つ挙げてみました。
(1)$\large\cos^2θ-\cosθ-\dfrac{3}{4}=0\ (0\leqqθ<2\pi)$
(2)$\large(\log_2x)^2-\log_2x^2-3=0$
(3)$\large5^{2x}-5^{x+1}-50=0$
(4)$\large x+2\sqrt{x}-8=0$」2022年4月18日
素因数分解を利用して最大公約数を求める
「$270,300,360$の最大公約数を求めよ。」
代表的な角度が出てこない三角方程式
「$0°\leqqθ<360°$のとき、上の方程式を解け。角度は小数第1位まで書くこと。」
2022年4月17日
素因数分解を利用して正の約数の個数・和を求める
「$504$の正の約数の個数を求めよ。」
2022年4月14日
素因数分解を利用して最小公倍数を求める
「$63,135,245$の最小公倍数を求めよ。」
2022年4月13日
なぜ位置を表す時間の関数x(t)を微分すると速度がわかるのか?
2022年4月12日
文字を含む分数の逆数を求めるには
分数の逆数は分子と分母を入れ替えるだけ、という簡単な方法で求めることができます。
しかし、$\dfrac{4}{3}x$のように分数と分子にも分母にも含まれない文字と組み合わさっている数の逆数はどのように求めるのでしょうか?
2022年4月11日
合成関数の微分
2022年4月10日
指数不等式を解く
\[\Large 5^{2x+2}-3\cdot5^{x+1}>11\cdot5^x-1\]
「上の不等式を解け。」
指数関数の大小関係、対数関数の大小関係
指数関数と対数関数の大小関係は、底がどんな値を取るのかで変わります。
2022年4月9日
多項式の関数の微分はなぜ項ごとの微分で求まるのか?
これは
なぜこれが成り立つのでしょうか?
絶対値が2つある1次関数
このような問題はどのように解けばよいでしょうか?
2022年4月8日
複素数の積・商
2022年4月7日
2022年4月6日
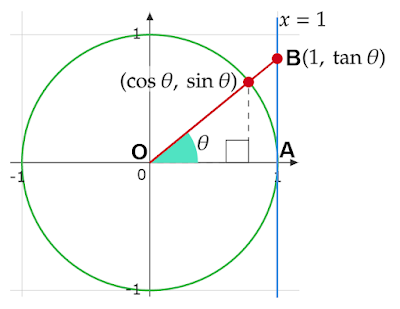
6つの三角関数を単位円上に表すと?
2022年4月5日
cscθ、secθ、cotθの相互関係
2022年4月4日
部分分数分解する方法
2022年4月3日
円に内接・外接する正二十角形、正三十角形、正六十角形の周の長さと円周率の関係
2022年3月31日
座標空間におけるベクトルの内積
2022年3月30日
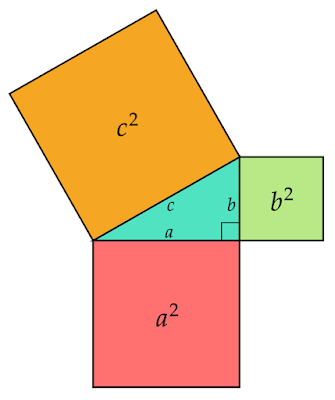
三平方の定理(ピタゴラスの定理)
三平方の定理は幾何学の有名な定理で直角三角形の3辺の長さの関係を表しています。
これを証明する方法は様々ありますが、一番簡単な方法は合同な直角三角形を4つ使って正方形を作る方法だと思います。
2022年3月29日
三角比で平行四辺形の面積を求める
なぜこの式で面積を求めることができるのでしょうか?
2022年3月27日
ピースを組み替えると面積が変わる?直角三角形
1年後の今日は何曜日?
(1)2022年1月1日
(2)2025年1月1日」2022年3月26日
平行四辺形の中の三角形の内角の大きさは?
このような問題はどのように解けばよいでしょうか?
帯分数で指数を含む計算をする
2022年3月24日
なぜ三角錐の体積は三角柱の体積の3分の1なのか?
三角錐の体積はなぜ三角柱の体積の$\dfrac{1}{3}$になるのでしょうか?
2022年3月20日
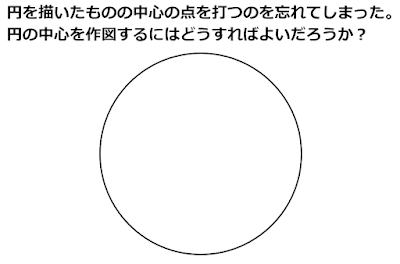
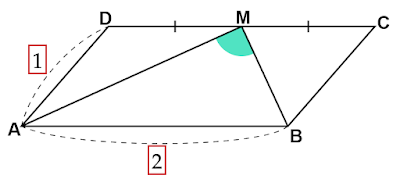
長さの測れないコンパスで長さの等しい線分を作図するには
このような問題はどのように解けばよいでしょうか?
2022年3月19日
正方行列と正則行列の違い
2022年3月18日
濃度の計算 正しく計算するには
(1)濃度$5$%の食塩水$120$gに食塩を$14$g加えると濃度は何%となるか?
(2)濃度$10$%の食塩水$80$gに水を$40$g加えると濃度は何%となるか?
(3)濃度$4$%の食塩水$70$gに濃度$8$%の食塩水$50$gを加えると濃度は何%となるか?」
このような問題はどのように解けばよいでしょうか?
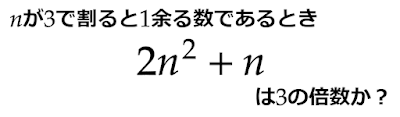
.png)
.png)
.png)
.png)
.png)
.png)
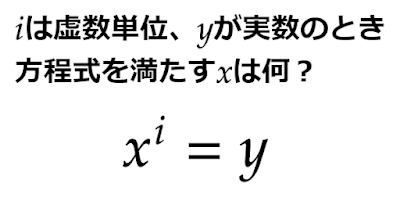
.png)
.png)
.png)
.png)
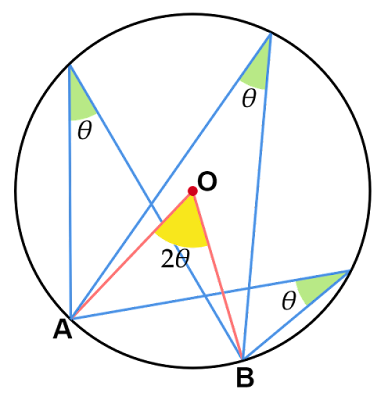
.png)



.png)
.png)
.png)
.png)